
【題目】列代數式或方程解應用題:
![]() 已知小明的年齡是
已知小明的年齡是![]() 歲,小紅的年齡比小明的年齡的
歲,小紅的年齡比小明的年齡的![]() 倍小
倍小![]() 歲,小華的年齡比小紅的年齡大
歲,小華的年齡比小紅的年齡大![]() 歲,求這三名同學的年齡的和.
歲,求這三名同學的年齡的和.
![]() 小亮與小明從學校同時出發去看在首都體育館舉行的一場足球賽, 小亮每分鐘走
小亮與小明從學校同時出發去看在首都體育館舉行的一場足球賽, 小亮每分鐘走![]() ,他走到足球場等了
,他走到足球場等了![]() 分鐘比賽才開始:小明每分鐘走
分鐘比賽才開始:小明每分鐘走![]() ,他走到足球場,比賽已經開始了
,他走到足球場,比賽已經開始了![]() 分鐘.問學校與足球場之間的距離有多遠?
分鐘.問學校與足球場之間的距離有多遠?
![]() 請根據圖中提供的信息,回答下列問題:
請根據圖中提供的信息,回答下列問題:

①一個水瓶與一個水杯分別是多少元?
②甲、乙兩家商場都銷售該水瓶和水杯,為了迎接新年,兩家商場都在搞促銷活動,甲商場規定:這兩種商品都打八折;乙商場規定:買一個水瓶贈送兩個水杯,單獨購買的水杯仍按原價銷售.若某單位想在一家商場買![]() 個水瓶和
個水瓶和![]() 個水杯,請問選擇哪家商場更合算?請說明理由.
個水杯,請問選擇哪家商場更合算?請說明理由.
【答案】(1)這三名同學的年齡的和是(5m﹣7)歲;(2)學校離足球場1920m;(3)①一個水瓶40元,一個水杯是8元;②選擇乙商場購買更合算.
【解析】
(1)根據題意分別列出小明、小紅和小華的年齡,再相加,去括號,合并同類項,即可求出這三名同學的年齡的和;
(2)設學校到足球場xm,根據時間=路程÷速度結合小亮比小明早到8分鐘,即可得出關于x的一元一次方程,解之即可得出結論;
(3)①設一個水瓶x元,表示出一個水杯為(48-x)元,根據題意列出方程,求出方程的解即可得到結果;
②計算出兩商場得費用,比較即可得到結果.
(1)解:∵小紅的年齡比小明的年齡的2倍小4歲,
∴小紅的年齡為(2m﹣4)歲.
又∵小華的年齡比小紅的年齡的大1歲,
∴小華的年齡為[(2m﹣4)+1](歲),·
∴這三名同學的年齡的和為m+(2m﹣4)+[(2m﹣4)+1]
=m+2m﹣4+2m﹣3
=(5m﹣7)歲.
答:這三名同學的年齡的和是(5m﹣7)歲.
(2)解:設學校到足球場xm,
根據題意得:![]() ﹣
﹣![]() =8,
=8,
解得:x=1920.
答:學校離足球場1920m.
(3)①設一個水瓶x元,表示出一個水杯為(48﹣x)元,
根據題意得:3x+4(48﹣x)=152,
解得:x=40,
則一個水瓶40元,一個水杯是8元;
②甲商場所需費用為(40×5+8×20)×80%=288(元);
乙商場所需費用為5×40+(20﹣5×2)×8=280(元),
∵288>280,
∴選擇乙商場購買更合算.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】“五一”期間,小明到小陳家所在的美麗鄉村游玩,在村頭A處小明接到小陳發來的定位,發現小陳家C在自己的北偏東45°方向,于是沿河邊筆直的綠道l步行200米到達B處,這時定位顯示小陳家C在自己的北偏東30°方向,如圖所示,根據以上信息和下面的對話,請你幫小明算一算他還需沿綠道繼續直走多少米才能到達橋頭D處(精確到1米)(備用數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,以△ABC的邊AB、AC向外作正方形ABDE和正方形ACFG,試判斷△ABC與△AEG面積之間的關系,并說明理由。

(2)園林小路,曲徑通幽,如圖2所示,小路由白色的正方形理石和黑色的三角形理石鋪成.已知中間的所有正方形的面積之和是a平方米,內圈的所有三角形的面積之和是b平方米,這條小路一共占地多少平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進了一批![]() 、
、![]() 兩種型號的智能掃地機器人,這兩種智能掃地機器人的進購數量、進價、售價如表所示:
兩種型號的智能掃地機器人,這兩種智能掃地機器人的進購數量、進價、售價如表所示:
類型 | 進購數量(個) | 進價(元/個) | 售價(元/個) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若該商場計劃全部銷售完這批智能掃地機器人的總利潤不少于32000元,則![]() 型智能掃地機器人的銷售單價至少是多少元?
型智能掃地機器人的銷售單價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
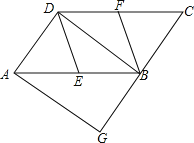
【題目】如圖,在平行四邊形ABCD中,E、F分別為邊AB、CD的中點,過A點作AG∥DB,交CB的延長線于點G.
(1)求證:DE∥BF;
(2)若∠G=90,求證:四邊形DEBF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
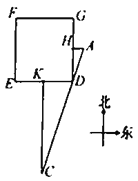
【題目】《九章算術》是中國傳統數學最重要的著作,在“勾股”章中有這樣一個問題:“今有邑方二百步,各中開門,出東門十五步有木,問:出南門幾步而見木?”
用今天的話說,大意是:如圖,![]() 是一座邊長為200步(“步”是古代的長度單位)的正方形小城,東門
是一座邊長為200步(“步”是古代的長度單位)的正方形小城,東門![]() 位于
位于![]() 的中點,南門
的中點,南門![]() 位于
位于![]() 的中點,出東門15步的
的中點,出東門15步的![]() 處有一樹木,求出南門多少步恰好看到位于
處有一樹木,求出南門多少步恰好看到位于![]() 處的樹木(即點
處的樹木(即點![]() 在直線
在直線![]() 上)?請你計算
上)?請你計算![]() 的長為__________步.
的長為__________步.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數![]() 交
交![]() 軸于點
軸于點![]() 、
、![]() ,交
,交![]() 軸于點
軸于點![]() ,在
,在![]() 軸上有一點
軸上有一點![]() ,連接
,連接![]() .
.
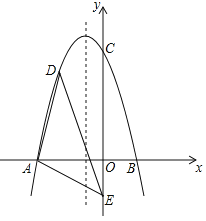
(1)求二次函數的表達式;
(2)若點![]() 為拋物線在
為拋物線在![]() 軸負半軸上方的一個動點,求
軸負半軸上方的一個動點,求![]() 面積的最大值;
面積的最大值;
(3)拋物線對稱軸上是否存在點![]() ,使
,使![]() 為等腰三角形,若存在,請直接寫出所有
為等腰三角形,若存在,請直接寫出所有![]() 點的坐標,若不存在請說明理由.
點的坐標,若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
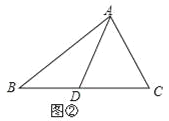
【題目】(1)如圖①,AD是△ABC的中線.△ABD與△ACD的面積有怎樣的數量關系?為什么?
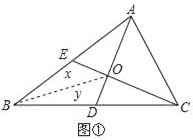
(2)若三角形的面積記為S,例如:△ABC的面積記為S△ABC.如圖②,已知S△ABC=1.△ABC的中線AD、CE相交于點O,求四邊形BDOE的面積.
小華利用(1)的結論,解決了上述問題,解法如下:
連接BO,設S△BEO=x,S△BDO=y,由(1)結論可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.則有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.則有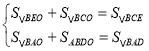 即
即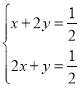 所以x+y=
所以x+y=![]() .即四邊形BDOE面積為
.即四邊形BDOE面積為![]() .
.
請仿照上面的方法,解決下列問題:
①如圖③,已知S△ABC=1.D、E是BC邊上的三等分點,F、G是AB邊上的三等分點,AD、CF交于點O,求四邊形BDOF的面積.
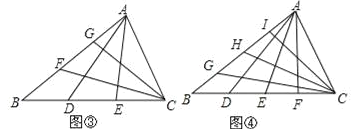
②如圖④,已知S△ABC=1.D、E、F是BC邊上的四等分點,G、H、I是AB邊上的四等分點,AD、CG交于點O,則四邊形BDOG的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知Rt△ABC,∠C=90°,AB=10,且cosA=![]() . M為線段AB的中點, 作DM⊥AB交AC于D. 點Q在線段AC上,點P在線段BC上,以PQ為直徑的圓始終過點M, 且PQ交線段DM于點E.
. M為線段AB的中點, 作DM⊥AB交AC于D. 點Q在線段AC上,點P在線段BC上,以PQ為直徑的圓始終過點M, 且PQ交線段DM于點E.
⑴ 試說明△AMQ∽△PME;
⑵ 當△PME是等腰三角形時,求出線段AQ的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com