
【題目】已知![]() 是
是![]() 的高,直線
的高,直線![]() 相交所成的角中有一個角為50°,則
相交所成的角中有一個角為50°,則![]() 的度數為________.
的度數為________.
 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:初中數學 來源: 題型:
【題目】(2015隨州)甲騎摩托車從A地去B地,乙開汽車從B地去A地,同時出發,勻速行駛,各自到達終點后停止,設甲、乙兩人間距離為s(單位:千米),甲行駛的時間為t(單位:小時),s與t之間的函數關系如圖所示,有下列結論:
①出發1小時時,甲、乙在途中相遇;
②出發1.5小時時,乙比甲多行駛了60千米;
③出發3小時時,甲、乙同時到達終點;
④甲的速度是乙速度的一半.
其中,正確結論的個數是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2﹣x+a(a>0),當自變量x取m時,其相應的函數值小于0,那么下列結論中正確的是( )
A.m﹣1>0
B.m﹣1<0
C.m﹣1=0
D.m﹣1與0的大小關系不確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九(2)班組織了一次朗讀比賽,甲、乙兩隊各10人的比賽成績(10分制)如下表(單位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲隊成績的中位數是分,乙隊成績的眾數是分;
(2)計算乙隊成績的平均數和方差;
(3)已知甲隊成績的方差是1.4分2 , 則成績較為整齊的是隊.
查看答案和解析>>
科目:初中數學 來源: 題型:
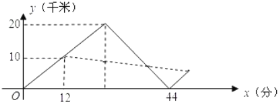
【題目】2018年5月,某城遭遇暴雨水災,武警戰士乘一沖鋒舟從A地逆流而上,前往C地營救受困群眾,途經B地時,由所攜帶的救生艇將B地受困群眾運回A地,沖鋒舟繼續前進,到C地接到群眾后立刻返回A地,途中曾與救生艇相遇,沖鋒舟和救生艇距A地的距離y(千米)和沖鋒舟出發后所用時間x(分)之間的函數圖象如圖所示,假設群眾上下沖鋒舟和救生艇的時間忽略不計,水流速度和沖鋒舟在靜水中的速度不變.
(1)沖鋒舟從A地到C地的時間為 分鐘,沖鋒舟在靜水中的速度為 千米/分,水流的速度為 千米/分.
(2)沖鋒舟將C地群眾安全送到A地后,又立即去接應救生艇,已知救生艇與A地的距離y(千米)和沖鋒舟出發后所用時間x(分鐘)之間的函數關系式為y=kx+b,若沖鋒舟在距離A地![]() 千米處與救生艇第二次相遇,求k、b的值.
千米處與救生艇第二次相遇,求k、b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,AD是∠BAC的角平分線,AE是△ABC的高.

(1)如圖1,若∠B=40°,∠C=62°,請說明∠DAE的度數;
(2)如圖2(∠B<∠C),試說明∠DAE、∠B、∠C的數量關系;
(3)如圖3,延長AC到點F,∠CAE和∠BCF的角平分線交于點G,求∠G的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司投資1200萬元購買了一條新生產線生產新產品.根據市場調研,生產每件產品需要成本50元,該產品進入市場后不得低于80元/件且不得超過160元/件,該產品銷售量y(萬件)與產品售價x(元)之間的關系如圖所示.
(1)求y與x之間的函數關系式,并寫出x的取值范圍;
(2)第一年公司是盈利還是虧損?求出當盈利最大或虧損最小時的產品售價;
(3)在(2)的前提下,即在第一年盈利最大或者虧損最小時,公司第二年重新確定產品售價,能否使前兩年盈利總額達790萬元?若能,求出第二年產品售價;若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,BD平分∠ABC,與AC交于點D,點O是AB上一點,⊙O過B、D兩點,且分別交AB、BC于點E、F.
(1)求證:AC是⊙O的切線;
(2)已知AB=10,BC=6,求⊙O的半徑r .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com