
【題目】如圖,ABCD的對角線AC、BD交于點O,AE平分∠BAD交BC于點E,且∠ADC=60°,AB= ![]() BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,連接OE.下列結論:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的個數有( )
BC,成立的個數有( )
A.1個
B.2個
C.3個
D.4個
【答案】C
【解析】∵四邊形ABCD是平行四邊形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等邊三角形,
∴AE=AB=BE,
∵AB= ![]() BC,
BC,
∴AE= ![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正確;
∵AC⊥AB,
∴SABCD=ABAC,故②正確,
∵AB= ![]() BC,OB=
BC,OB= ![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③錯誤;
∵CE=BE,CO=OA,
∴OE= ![]() AB,
AB,
∴OE= ![]() BC,故④正確.
BC,故④正確.
故答案為:C.
首先根據平行四邊形的性質可得到∠ABC=∠ADC=60°,∠BAD=120°,然后結合條件AE平分∠BAD,可得到∠BAE=∠EAD=60°,故此可證明△ABE是等邊三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正確;因為AC⊥AB,所以依據平行四邊形的面積公式可得到SABCD=ABAC,故②正確,然后由AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正確;因為AC⊥AB,所以依據平行四邊形的面積公式可得到SABCD=ABAC,故②正確,然后由AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,可證明AB≠OB,故③錯誤;接下來,依據三角形的中位線的性質定理證明OE=
BD,且BD>BC,可證明AB≠OB,故③錯誤;接下來,依據三角形的中位線的性質定理證明OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正確.
BC,故④正確.


科目:初中數學 來源: 題型:
【題目】如圖,已知AD∥BC,AE平分∠BAD,CD與AE相交于點F,∠CFE=∠E,試說明AB∥DC,把下面的說理過程補充完整.
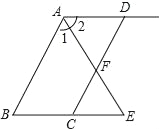
證明:∵AD∥BC(已知)
∴∠2=∠E(___________________________)
∵AE平分∠BAD(已知)
∴∠1=∠2 (_________________________)
∴∠1=∠E(___________________________)
∵∠CFE=∠E(已知)
∴∠1=∠______(______________________)
∴AB∥CD(_________________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,△ABC是等邊三角形,D、E分別為邊BC和AC上的點,且BD=CE,過D作BE的平行線,過E作BC的平行線,它們交于點F,連接AF.
(1)求證:△ABE≌△CAD;
(2)試判斷△ADF的形狀,并說明理由;
(3)若將D、E分別移為邊CB的延長線和AC的延長線上的點,其它條件不變(如圖②),則△ADF的形狀是否改變,說明理由.
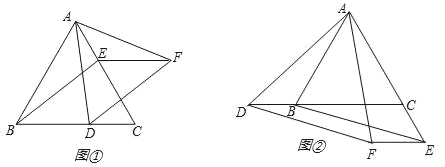
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在網格中,每個小正方形的邊長均為1個單位長度,我們將小正方形的頂點叫做格點,線段AB的端點均在格點上.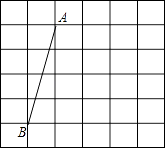
(1)將線段AB向右平移3個單位長度,得到線段A′B′,畫出平移后的線段并連接AB′和A′B,兩線段相交于點O;
(2)求證:△AOB≌△B′OA′.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春天來了,衢江河畔,鳥語花香,柳條搖曳.為給衢州市民提供更好的休閑鍛煉環境,決定對衢江沿河步行道修建改造.據了解我市步行道改造工程路線約12千米,若該任務由甲、乙兩工程隊先后接力完成,甲工程隊每天修建0.04千米,乙工程隊每天修建0.02千米,則兩工程隊共需修建500天,求甲、乙兩工程隊分別修建步行道多少千米.
根據題意,小剛同學列出了一個不完整的方程組![]() .
.
(1)根據小剛同學所列的方程組,請你分別指出未知數![]() ,
,![]() 表示的意義.
表示的意義.![]() 表示 ;
表示 ;![]() 表示 ;
表示 ;
(2)小紅同學的做法是:“設甲工程隊修建步行道![]() 千米,乙工程隊修建步行道
千米,乙工程隊修建步行道![]() 千米”,請你利用小紅同學設的未知數解決問題.
千米”,請你利用小紅同學設的未知數解決問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名工人同時加工同一種零件,現根據兩人7天產品中每天出現的次品數情況繪制成如下不完整的統計圖和表,依據圖、表信息,解答下列問題:
相關統計量表:
量數 人 | 眾數 | 中位數 | 平均數 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品數量統計表:
天數 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)補全圖、表.
(2)判斷誰出現次品的波動小.
(3)估計乙加工該種零件30天出現次品多少件?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 市首批一次性投放公共自行車700輛供市民租用出行,由于投入數量不夠, 導致出現需要租用卻未租到車的現象,現隨機抽取的某五天在同一時段的調查數據匯成如下表格.
市首批一次性投放公共自行車700輛供市民租用出行,由于投入數量不夠, 導致出現需要租用卻未租到車的現象,現隨機抽取的某五天在同一時段的調查數據匯成如下表格.
請回答下列問題:
時間 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行車卻未租到車的人數(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五個數據(人數)的中位數是多少?
(2)由隨機抽樣估計,平均每天在7:00-8:00 :需要租用公共自行車的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究:
(1)如圖①,點M、N分別為四邊形ABCD邊AD、BC的中點,則四邊形BNDM的面積與四邊形ABCD的面積關系是 . 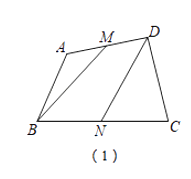
(2)如圖②,在四邊形ABCD中,點M、N分別為AD、BC的中點,MB交AN于點P,MC交DN于點Q,若S△四邊形MPNQ=10,則S△ABP+S△DCQ的值為多少?
(3)問題解決
在矩形ABCD中,AD=2,DC=4,點M、N為AB上兩點,且滿足BN=2AM=2MN,連接MC、MD.若點P為CD上任意一點,連接AP、NP,使得AP與DM交于點E,NP與MC交于點F,則四邊形MEPF的面積是否存最大值?若存在,請求出最大面積;若不存在,請說明理由.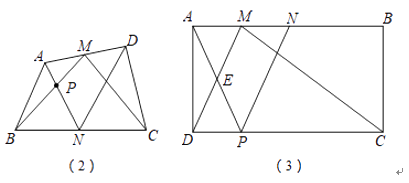
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D、E分別是AB、AC的中點,過點E作EF∥AB,交BC于點F.
(1)求證:四邊形DBFE是平行四邊形;
(2)當△ABC滿足什么條件時,四邊形DBEF是菱形?為什么?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com