
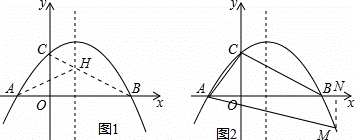
如圖,已知拋物線y= ﹣
﹣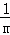 (x+2)(x﹣m)(m>0)與x軸相交于點A、B,與y軸相交于點C,且點A在點B的左側(cè).
(x+2)(x﹣m)(m>0)與x軸相交于點A、B,與y軸相交于點C,且點A在點B的左側(cè).
(1)若拋物線過點G(2,2),求實數(shù)m的值;
(2)在(1)的條件下,解答下列問題:
①求出△ABC的面積;
②在拋物線的對稱軸上找一點H,使AH+CH最小,并求出點H的坐標(biāo);
(3)在第四現(xiàn)象內(nèi),拋物線上是否存在點M,使得以點A、B、M為頂點的三角形與△ACB相似?若存在,求m的值;若不存在,請說明理由.
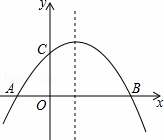
解:(1)∵拋物線過G(2,2),
∴把G坐標(biāo)代入拋物線解析式得:2=﹣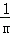 (2+2)(2﹣m),
(2+2)(2﹣m),
解得:m=4;
(2)①令y=0,得到﹣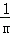 (x+2)(x﹣m)=0,
(x+2)(x﹣m)=0,
解得:x1=﹣2,x2=m,
∵m>0,
∴A(﹣2,0),B(m,0),
把m=4代入得:B(4,0),
∴AB=6,
令x=9,得到y(tǒng)=2,即C(0,2),
∴OC=2,
則S△ABC=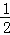 ×6×2=6;
×6×2=6;
②∵A(﹣2,0),B(4,0),
∴拋物線解析式為y=﹣ (x+2)(x﹣4)的對稱軸為x=1,
(x+2)(x﹣4)的對稱軸為x=1,
如圖1,連接BC交對稱軸于點H,由對稱軸的性質(zhì)和兩點之間線段最短的性質(zhì)可得:此時AH+CH=BH+CH=BC最小,
設(shè)直線BC的解析式為y=kx+b,
把B與C坐標(biāo)代入得: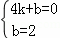 ,
,
解得: ,
,
∴直線BC解析式為y=﹣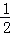 x+2,
x+2,
令x=1,得到y(tǒng)=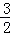 ,即H(1,
,即H(1,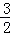 );
);
(3)在第 四現(xiàn)象內(nèi),拋物線上存在點M
四現(xiàn)象內(nèi),拋物線上存在點M ,使得以點A、B、M為頂點的三角形與△ACB相似,
,使得以點A、B、M為頂點的三角形與△ACB相似,
分兩種情況考慮:
(i)當(dāng)△ACB∽△ABM時,則有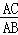 =
=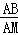 ,即AB2=AC•AM,
,即AB2=AC•AM,
∵A(﹣2,0),C(0,2),即OA=OC=2,
∴∠CAB=45°,∠BAM=45°,
如圖2,過M作MN⊥x軸,交x軸于點N,則AN=MN,
∴OA+ON=2+ON=MN,
設(shè)M(x,﹣x﹣2)(x>0),
把M坐標(biāo)代入拋物線解析式得:﹣x﹣2=﹣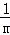 (x+2)(x﹣m),
(x+2)(x﹣m),
∵x>0,∴x+2>0,
∵m>0,∴x=2m,即M(2m,﹣2m﹣2),
∴AM=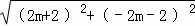 =2
=2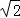 (m+1),
(m+1),
∵AB2=AC•AM,AC=2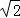 ,AB=m+2,
,AB=m+2,
∴(m+2)2=2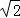 •2
•2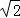 (m+1),
(m+1),
解得:m=2±2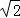 ,
,
∵m>0,
∴m=2+2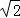 ;
;
(ii)當(dāng)△ACB∽△MBA時,則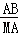 =
=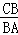 ,即AB2=CB•MA,
,即AB2=CB•MA,
∵∠CBA=∠BAM,∠ANM=∠BOC=90°,
∴△ANM∽△BOC,
∴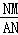 =
=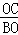 ,
,
∵OB=m,設(shè)ON=x,
∴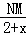 =
= ,即MN=
,即MN= (x+2),
(x+2),
令M(x,﹣ (x+2))(x>0),
(x+2))(x>0),
把M坐標(biāo)代入拋物線解析式得:﹣ (x+2)=﹣
(x+2)=﹣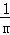 (x+2)(x﹣m),
(x+2)(x﹣m),
∵x>0,∴x+2>0,
∵m>0,∴x=m+2,即M(m+2,﹣ (m+4)),
(m+4)),
∵AB2=CB•MA,CB=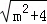 ,AN=m+4,MN=
,AN=m+4,MN=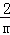 (m+4),
(m+4),
∴(m+2)2=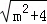 •
•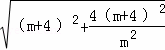 ,
,
整理得: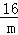 =0,顯然不成立,
=0,顯然不成立,
綜上,在第四象限內(nèi),當(dāng)m=2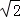 +2時,拋物線上存在點M,使得以點A、B、M為頂點的三角形與△ACB相似.
+2時,拋物線上存在點M,使得以點A、B、M為頂點的三角形與△ACB相似.


科目:初中數(shù)學(xué) 來源: 題型:
已知x=2是不等式 ≤0的解,且x=1不是這
≤0的解,且x=1不是這
個不等式的解,則實數(shù) 的取值范圍是 ( )
的取值范圍是 ( )
A、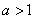 B、
B、 ≤2 C、
≤2 C、 ≤2 D、1≤
≤2 D、1≤ ≤2
≤2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
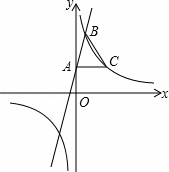
如圖,在平面直角坐標(biāo)系xOy中,一次函數(shù)y=3x+2的圖象與y軸交于點A,與反比例函數(shù)y= (k≠0)在第一象限內(nèi)的圖象交于點B,且點B的橫坐標(biāo)為1.過點A作AC⊥y軸交反比例函數(shù)y=
(k≠0)在第一象限內(nèi)的圖象交于點B,且點B的橫坐標(biāo)為1.過點A作AC⊥y軸交反比例函數(shù)y= (k≠0)的圖象于點C,連接BC.
(k≠0)的圖象于點C,連接BC.
(1)求反比例函數(shù)的表達式.
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
圖1是某中學(xué)九年級一班全體學(xué)生對三種水果喜歡人數(shù)的頻數(shù)分布 統(tǒng)計圖,根據(jù)圖中信息回答下列問題:
統(tǒng)計圖,根據(jù)圖中信息回答下列問題:
(1)九年級一班總?cè)藬?shù)是多少人?
(2)喜歡哪種水果人數(shù)的頻數(shù)最低?并求出該頻率;
(3)請根據(jù)頻數(shù)分布統(tǒng)計圖(圖1)的數(shù)據(jù),補全扇形統(tǒng)計圖(圖2);
(4)某水果攤位上正好只擺放有這三種水果出售,王阿姨去購買時,隨機購買其中兩種水果,恰好買到櫻桃和枇杷的概率是多少?用樹狀圖或列表說明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
下列命題正確的是( )
|
| A. | 矩形的對角線互相垂直 |
|
| B. | 兩邊和一角對應(yīng)相等的兩個三角形全等 |
|
| C. | 分式方程 |
|
| D. | 多項式t2﹣16+3t因式分解為(t+4)(t﹣4)+3t |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
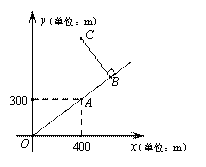
如圖是根據(jù)某公園的平面示意圖建立的平面直角坐標(biāo)系,公園的入口位于坐標(biāo)原點O,古塔位于點A(400,300),從古塔出發(fā)沿射線OA方向前行300m是盆景園B,從盆景園B向左轉(zhuǎn)90°后直行400m到達梅花閣C,則點C的坐標(biāo)是_______________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com