
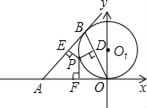
【題目】如圖,OB是以(O,a)為圓心,a為半徑的⊙O1的弦,過B點作⊙O1的切線,P為劣弧![]() 上的任一點,且過P作OB、AB、OA的垂線,垂足分別是D、E、F.
上的任一點,且過P作OB、AB、OA的垂線,垂足分別是D、E、F.
(1)求證:PD2=PEPF;
(2)當∠BOP=30°,P點為OB的中點時,求D、E、F、P四個點的坐標及S△DEF.
【答案】(1)詳見解析;(2)D(﹣![]() a,
a, ![]() a),E(﹣
a),E(﹣![]() a,
a, ![]() a),F(﹣
a),F(﹣![]() a,0),P(﹣
a,0),P(﹣![]() a,
a, ![]() );S△DEF=
);S△DEF=![]() a2.
a2.
【解析】試題分析:(1)連接PB,OP,利用AB切⊙O1于B求證△PBE∽△POD,得出![]() ,同理,△OPF∽△BPD,得出
,同理,△OPF∽△BPD,得出![]() ,然后利用等量代換即可.
,然后利用等量代換即可.
(2)連接O1B,O1P,得出△O1BP和△O1PO為等邊三角形,根據(jù)直角三角形的性質(zhì)即可解得D、E、F、P四個點的坐標.再利用三角形的面積公式可直接求出三角形DEF的面積.
試題解析:(1)證明:連接PB,OP,
∵PE⊥AB,PD⊥OB,
∴∠BEP=∠PDO=90°,
∵AB切⊙O1于B,∠ABP=∠BOP,
∴△PBE∽△POD,
∴![]() =
=![]() ,
,
同理,△OPF∽△BPD
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴PD2=PEPF;
(2)連接O1B,O1P,
∵AB切⊙O1于B,∠POB=30°,
∴∠ABP=30°,
∴∠O1BP=90°﹣30°=60°,
∵O1B=O1P,
∴△O1BP為等邊三角形,
∴O1B=BP,
∵P為弧BO的中點,
∴BP=OP,
即△O1PO為等邊三角形,
∴O1P=OP=a,
∴∠1OP=60°,
又∵P為弧BO的中點,
∴O1P⊥OB,
在△O1DO中,∵∠O1OP=60°O1O=a,
∴O1D=![]() a,OD=
a,OD=![]() a,
a,
過D作DM⊥OO1于M,∴DM=![]() OD=
OD=![]() a,
a,
OM=![]() DM=
DM=![]() a,
a,
∴D(﹣![]() a,
a,![]() a),
a),
∵∠O1OF=90°,∠O1OP=60°
∴∠POF=30°,
∵PE⊥OA,
∴PF=![]() OP=
OP=![]() a,OF=
a,OF=![]() a,
a,
∴P(﹣![]() a,
a,![]() ),F(﹣
),F(﹣![]() a,0),
a,0),
∵AB切⊙O1于B,∠POB=30°,
∴∠ABP=∠BOP=30°,
∵PE⊥AB,PB=a,
∴∠EPB=60°
∴PE=![]() a,BE=
a,BE=![]() a,
a,
∵P為弧BO的中點,
∴BP=PO,
∴∠PBO=∠BOP=30°,
∴∠BPO=120°,
∴∠BPE+∠BPO=120°+60°=180°,
即OPE三點共線,
∵OE=![]() a+a=
a+a=![]() a,
a,
過E作EM⊥x軸于M,∵AO切⊙O1于O,
∴∠EOA=30°,
∴EM=![]() OE=
OE=![]() a,OM=
a,OM=![]() a,
a,
∴E(﹣![]() a,
a,![]() a),
a),
∵E(﹣![]() a,
a,![]() a),D(﹣
a),D(﹣![]() a,
a,![]() a),
a),
∴DE=﹣![]() a﹣(﹣
a﹣(﹣![]() a)=
a)=![]() a,
a,
DE邊上的高為:![]() a,
a,
∴S△DEF=![]() ×
×![]() a×
a×![]() a=
a=![]() a2.
a2.
故答案為:D(﹣![]() a,
a,![]() a),E(﹣
a),E(﹣![]() a,
a,![]() a),F(﹣
a),F(﹣![]() a,0),P(﹣
a,0),P(﹣![]() a,
a,![]() );S△DEF=
);S△DEF=![]() a2.
a2.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC≌△DBE,點D在邊AC上,BC與DE交于點P.已知![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求∠CBE的度數(shù).
(2)求△CDP與△BEP的周長和.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(7分)如圖,EF//AD, ![]() =
=![]() .求證:∠DGA+∠BAC=180°.請將說明過程填寫完成.
.求證:∠DGA+∠BAC=180°.請將說明過程填寫完成.

證明:∵EF//AD,(已知)
∴![]() =_____(_____________________________).
=_____(_____________________________).
又∵![]() =
=![]() (______)
(______)
∴![]() =
=![]() (________________________).
(________________________).
∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() 是等邊三角形,
是等邊三角形,![]() 是
是![]() 邊上的一點,連接
邊上的一點,連接![]() ,把
,把![]() 繞著點
繞著點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() ,得到
,得到![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的周長是( )
的周長是( )

A.16B.15C.13D.12
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
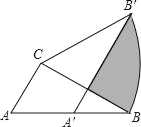
【題目】如圖,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.將△ABC繞點C逆時針旋轉(zhuǎn)α角后得到△A′B′C,當點A的對應點A'落在AB邊上時,旋轉(zhuǎn)角α的度數(shù)是_____度,陰影部分的面積為_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀材料:
學習了無理數(shù)、二次根式及完全平方公式后,某數(shù)學興趣小組開展了一次探究活動:
估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() ,
,
設(shè)![]() (0<k<1),
(0<k<1),
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() .
.
(1)請你用小明的方法估算![]() 的近似值(結(jié)果保留兩位小數(shù));
的近似值(結(jié)果保留兩位小數(shù));
(2)請你結(jié)合上述實例,概括出估算![]() 的公式:已知非負整數(shù)a,b,m,若
的公式:已知非負整數(shù)a,b,m,若![]() ,且
,且![]() ,則
,則![]() =_____________(用含a,b的代數(shù)式表示)
=_____________(用含a,b的代數(shù)式表示)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了預防疾病,某單位對辦公室采用藥熏消毒法進行消毒,已知藥物燃燒時,室內(nèi)每立方米空氣中的含藥量y(毫克)與時間x(分鐘)成為正比例,藥物燃燒后,y與x成反比例(如圖),現(xiàn)測得藥物8分鐘燃畢,此時室內(nèi)空氣中每立方米的含藥量6毫克,請根據(jù)題中所提供的信息,解答下列問題:

(1)藥物燃燒時,y關(guān)于x的函數(shù)關(guān)系式為________,自變量x的取值范為________;藥物燃燒后,y關(guān)于x的函數(shù)關(guān)系式為________.
(2)研究表明,當空氣中每立方米的含藥量低于1.6毫克時員工方可進辦公室,那么從消毒開始,至少需要經(jīng)過________分鐘后,員工才能回到辦公室;
(3)研究表明,當空氣中每立方米的含藥量不低于3毫克且持續(xù)時間不低于10分鐘時,才能有效殺滅空氣中的病菌,那么此次消毒是否有效?為什么?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校課外小組為了解同學們對學校“陽光跑操”活動的喜歡程度,抽取部分學生進行調(diào)查.被調(diào)查的每個學生按A(非常喜歡)、B(比較喜歡)、C(一般)、D(不喜歡)四個等級對活動評價.圖1和圖2是該小組采集數(shù)據(jù)后繪制的兩幅統(tǒng)計圖.經(jīng)確認扇形統(tǒng)計圖是正確的,而條形統(tǒng)計圖尚有一處錯誤且并不完整.請你根據(jù)統(tǒng)計圖提供的信息,解答下列問題:

(1)此次調(diào)查的學生人數(shù)為___;
(2)條形統(tǒng)計圖中存在錯誤的是___(填A. B.C中的一個),并在圖中加以改正;
(3)在圖2中補畫條形統(tǒng)計圖中不完整的部分;
(4)如果該校有600名學生,那么對此活動“非常喜歡”和“比較喜歡”的學生共有多少人?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com