【題目】如圖，在ABCD中，AM= 
AD，BD與MC相交于點O，則S△MOD：S△COD= ． 
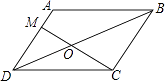
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】矩形OABC在平面直角坐標系中的位置如圖所示，點B的坐標為（3，4），D是OA的中點，點E在AB上，當△CDE的周長最小時，點E的坐標為（ ）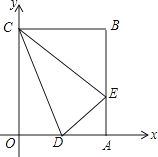 
A.（3，1）
B.（3， 
）
C.（3， 
）
D.（3，2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在⊙O中，AB為直徑，C為⊙O上一點．
（1）如圖1．過點C作⊙O的切線，與AB的延長線相交于點P，若∠CAB=27°，求∠P的大小；
（2）如圖2，D為 
上一點，且OD經過AC的中點E，連接DC并延長，與AB的延長線相交于點P，若∠CAB=10°，求∠P的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，兩個同心圓，大圓的弦AB與小圓相切于點P，大圓的弦CD經過點P，且CD=13，PD=4，則兩圓組成的圓環的面積是（ ）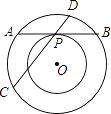 
A.16π
B.36π
C.52π
D.81π
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知，⊙O為△ABC的外接圓，BC為直徑，點E在AB上，過點E作EF⊥BC，點G在FE的延長線上，且GA=GE． 
（1）求證：AG與⊙O相切．
（2）若AC=6，AB=8，BE=3，求線段OE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
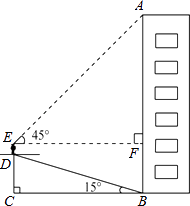
【題目】小華為了測量樓房AB的高度，他從樓底的B處沿著斜坡向上行走20m，到達坡頂D處．已知斜坡的坡角為15°．小華的身高ED是1.6m，他站在坡頂看樓頂A處的仰角為45°，求樓房AB的高度．（計算結果精確到1m） （參考數據：sin15°= 
，cos15°= 
，tan15°= 
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點O為坐標原點，A，B，C三點的坐標為（ 
，0）、（3 ，0）、（0，5），點D在第一象限，且∠ADB=60°，則線段CD的長的最小值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，以BC為半徑作⊙B，交AB于點D，交AB的延長線于點E，連接CD、CE．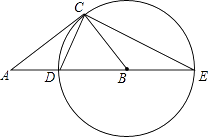 
（1）求證：△ACD∽△AEC；
（2）當 
= 
時，求tanE；
（3）若AD=4，AC=4 
，求△ACE的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC是等腰直角三角形，∠A=90°，BC=4，點P是△ABC邊上一動點，沿B→A→C的路徑移動，過點P作PD⊥BC于點D，設BD=x，△BDP的面積為y，則下列能大致反映y與x函數關系的圖象是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
