
【題目】如圖,在平行四邊形ABCD和平行四邊形AECF的頂點,D,E,F,B在一條直線上,則下列等式成立的是( )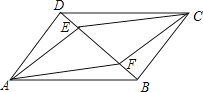
A.AE=CE
B.CE=CF
C.DE=BF
D.DE=EF=BF
【答案】C
【解析】
平行四邊形的對比平行且相等,所以AB=DC,AD=BC,所以∠ABD=∠CDF,∠AEB=∠CFD,所以易證△AEB≌△CFD,故各個結論可證.
∵四邊形AECF是平行四邊形
∴AE=CF,CE=AF(∴A、B不成立)
∵在平行四邊形AECF和平行四邊形ABCD中,AE∥CF,AB∥CD
∴∠ABD=∠CDF,∠AEB=∠CFD
∵AB=CD
∴△AEB≌△CFD
∴DF=BE
∴DE=BF(∴C成立,D不成立)
故選C.
【考點精析】關于本題考查的平行四邊形的性質,需要了解平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】某超市計劃經銷一些特產,經銷前,圍繞“A:王高虎頭雞,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鴨蛋”四種特產,在全市范圍內隨機抽取了部分市民進行問卷調查:“我最喜歡的特產是什么?”(必選且只選一種).現將調查結果整理后,繪制成如圖所示的不完整的扇形統計圖和條形統計圖.

(1)請補全扇形統計圖和條形統計圖;
(2)若全市有110萬市民,估計全市最喜歡“羊口咸蟹子”的市民約有多少萬人?
(3)在一個不透明的口袋中有四個分別寫上四種特產標記A、B、C、D的小球(除標記外完全相同),隨機摸出一個小球然后放回,混合搖勻后,再隨機摸出一個小球,則兩次都摸到A的概率是多少?寫出分析計算過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠第一季度的電費為![]() 元,水費比電費的2倍多30元.第二季度電費比第一季度節約了30%,水費比第一季度多支出了30%.
元,水費比電費的2倍多30元.第二季度電費比第一季度節約了30%,水費比第一季度多支出了30%.
(1)該工廠第二季度水電費(電費與水費之和)為多少元?
(2)該工廠第二季度水電費與第一季度水電費相比,是增加了還是減少了?增加或減少了多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年10月12日至15日,第二屆中國“互聯網+”大學生創新創業全國總決賽上,ofo共享單車從全國約119000個創業項目中脫穎而出,最終獲得金獎. 將119000用科學計數法表示應為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知鈍角△ABC,老師按照如下步驟尺規作圖:
步驟1:以C為圓心,CA為半徑畫弧①;
步驟2:以B為圓心,BA為半徑畫弧②,交弧①于點D;
步驟3:連接AD,交BC延長線于點H .
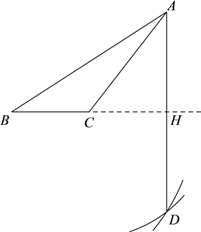
小明說:圖中的BH⊥AD且平分AD.
小麗說:圖中AC平分∠BAD.
小強說:圖中點C為BH的中點.
他們的說法中正確的是___________.他的依據是_____________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【閱讀理解】
我們知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2結果等于多少呢?
,那么12+22+32+…+n2結果等于多少呢?
在圖1所示三角形數陣中,第1行圓圈中的數為1,即12,第2行兩個圓圈中數的和為2+2,即22,…;第n行n個圓圈中數的和為![]() ,即n2,這樣,該三角形數陣中共有
,即n2,這樣,該三角形數陣中共有![]() 個圓圈,所有圓圈中數的和為12+22+32+…+n2.
個圓圈,所有圓圈中數的和為12+22+32+…+n2.


【規律探究】
將三角形數陣經兩次旋轉可得如圖2所示的三角形數陣,觀察這三個三角形數陣各行同一位置圓圈中的數(如第n﹣1行的第一個圓圈中的數分別為n﹣1,2,n),發現每個位置上三個圓圈中數的和均為 ,由此可得,這三個三角形數陣所有圓圈中數的總和為:3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
【解決問題】
根據以上發現,計算: ![]() 的結果為 .
的結果為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com