
【題目】將兩塊全等的三角板如圖①擺放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)將圖①中的△A1B1C順時針旋轉45°得圖②,點P1是A1C與AB的交點,點Q是A1B1與BC的交點,求證:CP1=CQ;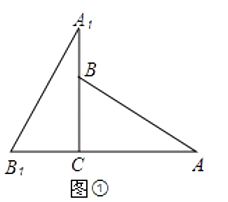
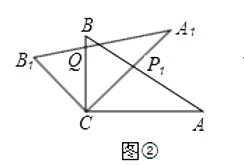
(2)在圖②中,若AP1=2,則CQ等于多少?
(3)如圖③,在B1C上取一點E,連接BE、P1E,設BC=1,當BE⊥P1B時,求△P1BE面積的最大值.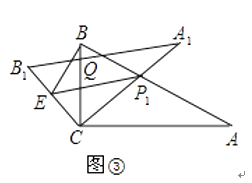
【答案】
(1)證明:∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°,
∵在△B1CQ和△BCP1中,
 ,
,
∴△B1CQ≌△BCP1(ASA),
∴CQ=CP1
(2)解:作P1D⊥CA于D,
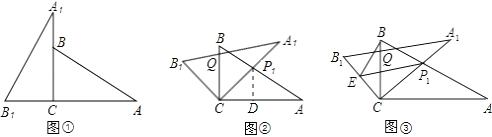
∵∠A=30°,
∴P1D= ![]() AP1=1,
AP1=1,
∵∠P1CD=45°,
∴ ![]() =sin45°=
=sin45°= ![]() ,
,
∴CP1= ![]() P1D=
P1D= ![]() ,
,
又∵CP1=CQ,
∴CQ= ![]()
(3)解:∵∠P1BE=90°,∠ABC=60°,
∴∠A=∠CBE=30°,
∴AC= ![]() BC,
BC,
由旋轉的性質可得:∠ACP1=∠BCE,
∴△AP1C∽△BEC,
∴AP1:BE=AC:BC= ![]() :1,
:1,
設AP1=x,則BE= ![]() x,
x,
在Rt△ABC中,∠A=30°,
∴AB=2BC=2,
∴S△P1BE= ![]() ×
× ![]() x(2﹣x)=﹣
x(2﹣x)=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
故當x=1時,S△P1BE(max)= ![]()
【解析】(1)根據旋轉的性質,易證得△B1CQ≌△BCP1,即可得到CQ=CP1。
(2)由(1)結論可知CQ=CP1。要求CQ的長,只需求出CP1的長,添加輔助線,將CP1轉化到直角三角形中,作P1D⊥CA于D,根據∠A=30°,可求出P1D的長,然后在Rt△P1DC中,可求出CP1的長,即可得出結論。
(3)根據旋轉的性質,先證明△AP1C∽△BEC,得對應邊成比例,建立方程,用含x的代數式分別表示出AP1、BE的長,在Rt△ABC中,求出AB的長,即可求出S△P1BE與x的函數關系式,求出頂點坐標,即可得到△P1BE面積的最大值。
【考點精析】根據題目的已知條件,利用二次函數的最值和相似三角形的判定與性質的相關知識可以得到問題的答案,需要掌握如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


科目:初中數學 來源: 題型:
【題目】如圖,從熱氣球C上測得兩建筑物A,B底部的俯角分別為30°和60度.如果這時氣球的高度CD為90米.且點A,D,B在同一直線上,求建筑物A,B間的距離.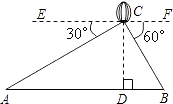
查看答案和解析>>
科目:初中數學 來源: 題型:
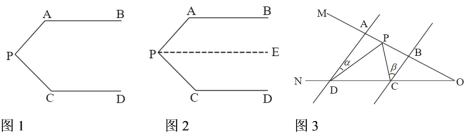
【題目】(1)同題情景:如圖1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度數.
小明想到一種方法,但是沒有解答完:
如圖2,過P作PE//AB,∴∠APE+∠PAB=180°,
∴∠APE=180°-∠PAB=180°-130°=50°
∵AB//CD,∴PE//CD.
……
請你幫助小明完成剩余的解答.
(2)問題遷移:請你依據小明的解題思路,解答下面的問題:
如圖3,AD//BC,當點P在A、B兩點之間時,∠ADP=∠α,∠BCP=∠β,則∠CPD,∠α,∠β之間有何數量關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
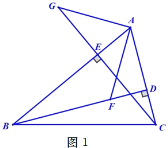
【題目】如圖,在△ABC中,BD,CE分別是AC,AB邊上的高,在BD上截取BF=AC,延長CE至點G使CG=AB,連接AF,AG.
(1)如圖1,求證:AG=AF;
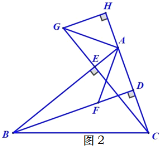
(2)如圖2,若BD恰好平分∠ABC,過點G作GH⊥AC交CA的延長線于點H,請直接寫出圖中所有的全等三角形并用全等符號連接.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,∠ABC的平分線交AC于點D,點O是AB上一點,⊙O過B、D兩點,且分別交AB,BC于點E,F.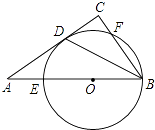
(1)求證:AC是⊙O的切線;
(2)已知AB=5,AC=4,求⊙O的半徑r.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為13cm,弦AB∥CD,AB=24cm,CD=10cm,則AB,CD之間的距離為( )
A.17cm
B.7cm
C.12cm
D.17cm或7cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小麗的家和學校在一條筆直的馬路旁,某天小麗沿著這條馬路去上學,她先從家步行到公交站臺甲,再乘車到公交站臺乙下車,最后步行到學校(在整個過程中小麗步行的速度不變),圖中的折線ABCDE表示小麗和學校之間的距離y(米)與她離家的時間x(分)之間的函數關系.
(1)求小麗步行的速度及學校與公交站臺乙之間的距離;
(2)當8≤x≤15時,求y與x之間的函數解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠生產一種產品,當生產數量至少為10噸,但不超過50噸時,每噸的成本y(萬元/噸)與生產數量x(噸)的函數關系的圖象如圖所示.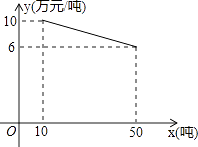
(1)求y關于x的函數解析式,并寫出x的取值范圍;
(2)當生產這種產品每噸的成本為7萬元時,求該產品的生產數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在10×10的正方形網格中,每個小正方形的邊長為1個單位長度.△ABC的頂點都在正方形網格的格點上,且通過兩次平移(沿網格線方向作上下或左右平移)后得到△![]() ,點C的對應點是直線上的格點
,點C的對應點是直線上的格點![]() .
.
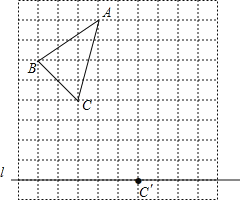
(1)畫出△![]() .
.
(2)若連接![]() 、
、![]() ,則這兩條線段之間的關系是 .
,則這兩條線段之間的關系是 .
(3)試在直線![]() 上畫出所有符合題意的格點P,使得由點
上畫出所有符合題意的格點P,使得由點![]() 、
、![]() 、
、![]() 、P四點圍成的四邊形的面積為9.
、P四點圍成的四邊形的面積為9.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com