Question

已知反比例函數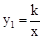的圖象與一次函數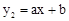的圖象交于點A（1，4）和點B

（，）．

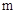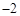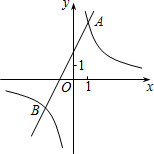
（1）求這兩個函數的表達式；

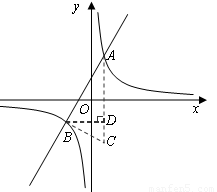
（2）觀察圖象，當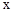>0時，直接寫出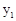>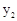時自變量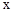的取值范圍；

（3）如果點C與點A關于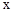軸對稱，求△ABC的面積．

 

Answer 1

【答案】

解：（1）∵點A（1，4）在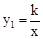的圖象上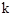，∴＝1×4＝4。

∴反比例函數的表達式為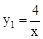 

∵點B在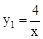的圖象上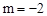，∴ 。∴點B（－2，－2）。

又∵點A、B在一次函數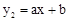的圖象上，

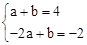∴   ，解得 。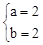

∴一次函數的表達式為。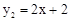 

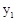（2）由圖象可知，當 0＜＜1時，＞成立       

（3）∵點C與點A關于軸對稱，∴C（1，－4）。

過點B作BD⊥AC，垂足為D，則D（1，－5）。  

∴△ABC的高BD＝1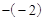＝3，底為AC＝4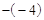＝8。

∴S_△ABC=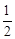AC·BD=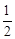×8×3=12。 

【解析】（1）根據點A的坐標求出反比例函數的解析式為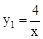，再求出B的坐標是（－2，－2），利用待定系數法求一次函數的解析式。

（2）當一次函數的值小于反比例函數的值時，直線在雙曲線的下方，直接根據圖象寫出當>0時，一次函數的值小于反比例函數的值x的取值范圍或0＜x＜1。

（3）根據坐標與線段的轉換可得出：AC、BD的長，然后根據三角形的面積公式即可求出答案。