Question

我們發現，用不同的方式表示同一圖形的面積可以解決線段長度之間關系的有關問題這種方法稱為等面積法，這是一種重要的數學方法．請你用等面積法來探究下列兩個問題：

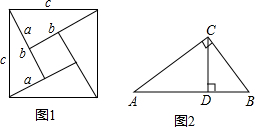
（1）如圖1是著名的趙爽弦圖，由四個全等的直角三角形拼成，請你用它來驗證勾股定理；

（2）如圖2，在Rt△ABC中，∠ACB=90°，CD是AB邊上的高，AC= 4，BC=3，求CD的長度．

 

Answer 1

【答案】

（1）見解析；（2）

【解析】本題考查了勾股定理的證明和對三角形和正方形面積公式的熟練掌握和運用

（1）根據題意，我們可在圖中找等量關系，由中間的小正方形的面積等于大正方形的面積減去四個直角三角形的面積，列出等式化簡即可得出勾股定理的表達式．

（2）先由勾股定理求出AB的長，再根據三角形的面積求CD的長即可．

（1）∵大正方形面積為c²，直角三角形面積為 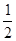ab，小正方形面積為：（b－a）²，

∴ c² = 4×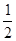ab+（a-b）² = 2ab + a²-2ab+b²，即c² = a²+b²．

（2）在Rt△ABC中，

∵∠ACB=90°,

∴由勾股定理，得： 

∵ CD⊥AB,

∴ S_△ABC =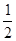AC·BC=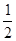AB·CD

∴ CD =