分析:(1)原式第一項表示1的2012次冪的相反數,第二項利用負指數公式化簡,第三項利用零指數公式化簡,最后一項先利用二次根式的化簡公式及特殊角的三角函數值化簡,再利用絕對值的代數意義化簡,合并即可得到結果;
(2)找出方程的最簡公分母為(x+1)(x-1),方程兩邊都乘以最簡公分母,化為整式方程,求出方程的解得到x的值,經檢驗即可得到原分式方程的解;
(3)將原式被除式中兩項通分并利用同分母分式的加法法則計算,除式分子利用平方差公式分解因式,分母利用完全平方公式分解因式,然后利用除以一個數等于乘以這個數的倒數將除法運算化為乘法運算,約分得到最簡結果,將a的值代入化簡后的式子中計算,即可得到原式的值.
解答:解:(1)原式=-1+4-1+|3
-8×
|=-1+4-1+
=2+
;
(2)方程化為
-
=1,
方程兩邊同時乘以(x+1)(x-1)得:6-3(x+1)=(x+1)(x-1),
整理得:x
2+3x-4=0,即(x-1)(x+4)=0,
可得x-1=0或x+4=0,
解得:x
1=1,x
2=-4,
代入方程檢驗,1為增根,-4是原方程的解;
(3)原式=
÷
=
•
=a-2,
當a=2+
時,原式=2+
-2=
.
點評:此題考查了分式的化簡求值,以及實數的混合運算,分式的加減運算關鍵是通分,通分的關鍵是找最簡公分母;分式的乘除運算關鍵是約分,約分的關鍵是找公因式,約分時,分式的分子分母出現多項式,應將多項式分解因式后再約分.



 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案 (2012•成都模擬)設函數y=x2-(2k+1)x+2k-4的圖象如圖所示,它與x軸交于A,B兩點,且線段OA與OB的長度之比為1:3,則k=
(2012•成都模擬)設函數y=x2-(2k+1)x+2k-4的圖象如圖所示,它與x軸交于A,B兩點,且線段OA與OB的長度之比為1:3,則k=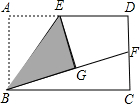 (2012•成都模擬)如圖,在矩形ABCD中,E是AD的中點,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,再延長BG交DC于點F.
(2012•成都模擬)如圖,在矩形ABCD中,E是AD的中點,將△ABE沿BE折疊后得到△GBE,且點G在矩形ABCD內部,再延長BG交DC于點F.