
【題目】已知拋物線L:y=![]() x2+bx﹣2與x軸相交于A、B兩點(點A在點B的左側),并與y軸相交于點C.且點A的坐標是(﹣1,0).
x2+bx﹣2與x軸相交于A、B兩點(點A在點B的左側),并與y軸相交于點C.且點A的坐標是(﹣1,0).
(1)求該拋物線的函數表達式及頂點D的坐標;
(2)判斷△ABC的形狀,并求出△ABC的面積;
(3)將拋物線向左或向右平移,得到拋物線L′,L′與x軸相交于A'、B′兩點(點A′在點B′的左側),并與y軸相交于點C′,要使△A'B′C′和△ABC的面積相等,求所有滿足條件的拋物線的函數表達式.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2,頂點D的坐標為(
x﹣2,頂點D的坐標為(![]() ,﹣
,﹣![]() );(2)△ABC是直角三角形,△ABC的面積是5;(3)所有滿足條件的拋物線的函數表達式是y=
);(2)△ABC是直角三角形,△ABC的面積是5;(3)所有滿足條件的拋物線的函數表達式是y=![]() ,y=
,y=![]() ,y=
,y=![]() .
.
【解析】
(1)根據拋物線過點A可以求得拋物線的解析式,然后將拋物線化為頂點式即可得到頂點D的坐標;
(2)根據(1)中的函數解析式可以求得點A、B、C的坐標,從而可以判斷△ABC的形狀并求出它的面積;
(3)根據平移的特點和分類討論的方法可以求得相應的函數解析式.
(1)∵拋物線L:y=![]() x2+bx﹣2過點A(﹣1,0),
x2+bx﹣2過點A(﹣1,0),
∴0=![]() ×(﹣1)2+b×(﹣1)﹣2,
×(﹣1)2+b×(﹣1)﹣2,
解得,b=﹣![]() ,
,
∴y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() ,
,
∴點D的坐標為(![]() ,﹣
,﹣![]() ),
),
即該拋物線的函數表達式是y=![]() x2﹣
x2﹣![]() x﹣2,頂點D的坐標為(
x﹣2,頂點D的坐標為(![]() ,﹣
,﹣![]() );
);
(2)當y=0時,0=![]() x2﹣
x2﹣![]() x﹣2,解得,x1=﹣1,x2=4,當x=0時,y=﹣2,
x﹣2,解得,x1=﹣1,x2=4,當x=0時,y=﹣2,
則點A(﹣1,0),點B(4,0),點C(0,﹣2),
∴AB=5,AC=![]() ,BC=2
,BC=2![]() ,
,
∵AB2=AC2+BC2,
∴△ABC是直角三角形,
∴△ABC的面積是:![]() =5;
=5;
(3)∵拋物線向左或向右平移,
∴平移后A′B′與平移前的AB的長度相等,
∴只要平移后過(0,﹣2)或過(0,2)即滿足條件,
當向右平移時,
令y=![]() ,當x=0時,y=
,當x=0時,y=![]() =2,得a=
=2,得a=![]() ,
,
此時y=![]() =
=![]() ,
,
當向左平移時,
令y=![]() ,當x=0時,y=
,當x=0時,y=![]() =±2,得m=
=±2,得m=![]() 或m=3,
或m=3,
當m=![]() 時,y=
時,y=![]() ,當m=3時,y=
,當m=3時,y=![]() ﹣2,
﹣2,
由上可得,所有滿足條件的拋物線的函數表達式是y=![]() ,y=
,y=![]() ,y=
,y=![]() ﹣2.
﹣2.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
【題目】拋擲兩枚普通的正方體骰子,把兩枚骰子的點數相加,若第一枚骰子的點數為1,第二枚骰子的點數為5,則是“和為6”的一種情況,我們按順序記作(1,5),如果一個游戲規定擲出“和為6”時甲方贏,擲出“和為9”時乙方贏,則這個游戲________(填“公平”、“不公平”).
查看答案和解析>>
科目:初中數學 來源: 題型:
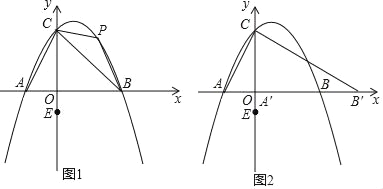
【題目】如圖,在平面直角坐標系中,拋物線y=﹣![]() x2+x+2
x2+x+2![]() 與x軸交于A、B兩點,交y軸于點C,點C關于拋物線對稱軸的對稱點為點D.
與x軸交于A、B兩點,交y軸于點C,點C關于拋物線對稱軸的對稱點為點D.
(1)求線段AC的長度;
(2)P為線段BC上方拋物線上的任意一點,點E為(0,﹣1),一動點Q從點P出發運動到y軸上的點G,再沿y軸運動到點E.當四邊形ABPC的面積最大時,求PG+![]() GE的最小值;
GE的最小值;
(3)將線段AB沿x軸向右平移,設平移后的線段為A'B',直至A'P平行于y軸(點P為第2小問中符合題意的P點),連接直線CB'.將△AOC繞著O旋轉,設旋轉后A、C的對應點分別為A'、C',在旋轉過程中直線A'C'與y軸交于點M,與線段CB'交于點N.當△CMN是以MN為腰的等腰三角形時,寫出CM的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
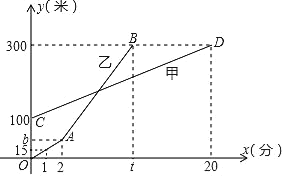
【題目】甲、乙兩人相約周末登花果山,甲、乙兩人距地面的高度y(米)與登山時間x(分)之間的函數圖象如圖所示,根據圖象所提供的信息解答下列問題:
(1)甲登山上升的速度是每分鐘 米,乙在A地時距地面的高度b為 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,請求出乙登山全程中,距地面的高度y(米)與登山時間x(分)之間的函數關系式;
(3)登山多長時間時,甲、乙兩人距地面的高度差為70米?
查看答案和解析>>
科目:初中數學 來源: 題型:
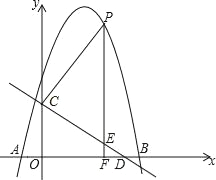
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于A(﹣1,0),B(5,0)兩點,直線y=﹣![]() x+3與y軸交于點C,與x軸交于點D.點P是直線CD上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
x+3與y軸交于點C,與x軸交于點D.點P是直線CD上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
(1)求拋物線的解析式;
(2)求PE的長最大時m的值.
(3)Q是平面直角坐標系內一點,在(2)的情況下,以PQCD為頂點的四邊形是平行四邊形是否存在?若存在,直接寫出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
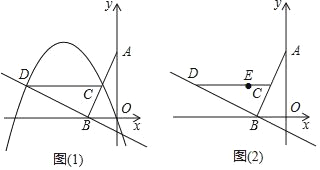
【題目】已知在平面直角坐標系xOy中,O為坐標原點,線段AB的兩個端點的坐標分別為A (0,2),B(﹣1,0),點C為線段AB的中點,現將線段BA繞點B按逆時針方向旋轉90°得到線段BD,拋物線y=ax2+bx+c(a≠0)、經過點D.
(1)如圖1,若該拋物線經過原點O,且a=﹣1.
①求點D的坐標及該拋物線的解析式;
②連結CD,問:在拋物線上是否存在點P,使得∠POB與∠BCD互余?若存在,請求出所有滿足條件的點P的坐標,若不存在,請說明理由.
(2)如圖2,若該拋物線y=ax2+bx+c(a<0)經過點E(﹣1,1),點Q在拋物線上,且滿足∠QOB與∠BCD互余,若符合條件的Q點的個數是4個,請直接寫出a的取值范圍 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某藍莓種植生產基地產銷兩旺,采摘的藍莓部分加工銷售,部分直接銷售,且當天都能銷售完,直接銷售是40元/斤,加工銷售是130元/斤(不計損耗).已知基地雇傭20名工人,每名工人只能參與采摘和加工中的一項工作,每人每天可以采摘70斤或加工35斤.設安排x名工人采摘藍莓,剩下的工人加工藍莓.
(1)若基地一天的總銷售收入為y元,求y與x的函數關系式;
(2)試求如何分配工人,才能使一天的銷售收入最大?并求出最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
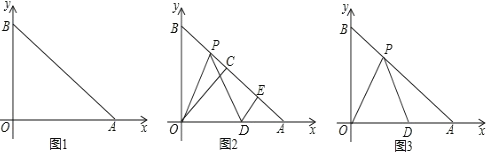
【題目】如圖1在平面直角坐標系中,![]() 、
、![]() ,
,![]() 滿足
滿足![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一動點,
上一動點,![]() 是
是![]() 軸正半軸上一點,且
軸正半軸上一點,且![]() ,
,![]() 于
于![]() .
.
(1)求![]() 的度數;
的度數;
(2)如圖2,設![]() ,當點
,當點![]() 運動時,
運動時,![]() 的值是否變化?若變化,說明理由;若不變,請求
的值是否變化?若變化,說明理由;若不變,請求![]() 的值;
的值;
(3)如圖3,設![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com