
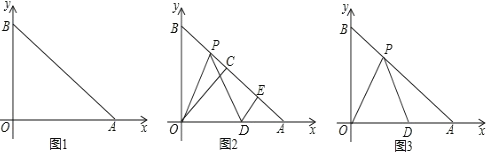
【題目】如圖1在平面直角坐標系中,![]() 、
、![]() ,
,![]() 滿足
滿足![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一動點,
上一動點,![]() 是
是![]() 軸正半軸上一點,且
軸正半軸上一點,且![]() ,
,![]() 于
于![]() .
.
(1)求![]() 的度數;
的度數;
(2)如圖2,設![]() ,當點
,當點![]() 運動時,
運動時,![]() 的值是否變化?若變化,說明理由;若不變,請求
的值是否變化?若變化,說明理由;若不變,請求![]() 的值;
的值;
(3)如圖3,設![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
【答案】(1)∠OAB=45°;(2)PE的值不變.理由見解析;(3)D(6![]() 6,0).
6,0).
【解析】
(1)根據非負數的性質即可求得a,b的值,從而得到△AOB是等腰直角三角形,據此即可求得;
(2)根據等腰三角形的性質以及三角形的外角的性質可以得到∠POC=∠DPE,即可證得△POC≌△DPE,則OC=PE,OC的長度根據等腰直角三角形的性質可以求得;
(3)利用等腰三角形的性質,以及外角的性質證得∠POC=∠DPE,即可證得△POC≌△DPE,根據全等三角形的對應邊相等,即可求得OD的長,從而求得D的坐標.
(1)根據題意得:
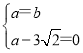 ,
,
解得:a=b=3![]() ,
,
∴OA=OB,
又∵∠AOB=90°
∴△AOB為等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不變.理由如下:
∵△AOB為等腰直角三角形,且AC=BC,
∴∠AOC=∠BOC=45°
又∵OC⊥AB于C,
∵PO=PD
∴∠POD=∠PDO
當P在BC上時,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,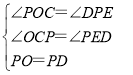 ,
,
∴△POC≌△DPE,
∴OC=PE
又OC=![]() AB=3
AB=3
∴PE=3;
當P在AC上時,∠POD=45°-∠POC,∠PDO=45°-∠DPE,
則∠POC=∠DPE.
同理可得PE=3;
(3)∵OP=PD,
∴∠POD=∠PDO=![]() =67.5°,
=67.5°,
則∠PDA=180°-∠PDO=180°-67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO
則在△POB和△DPA中, ,
,
∴△POB≌△DPA(AAS).
∴PA=OB=3![]() ,
,
∴DA=PB=6-3![]() ,
,
∴OD=OA-DA=3![]() -(6-3
-(6-3![]() )=6
)=6![]() -6
-6
∴D(6![]() 6,0).
6,0).


 激活思維優加課堂系列答案
激活思維優加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線L:y=![]() x2+bx﹣2與x軸相交于A、B兩點(點A在點B的左側),并與y軸相交于點C.且點A的坐標是(﹣1,0).
x2+bx﹣2與x軸相交于A、B兩點(點A在點B的左側),并與y軸相交于點C.且點A的坐標是(﹣1,0).
(1)求該拋物線的函數表達式及頂點D的坐標;
(2)判斷△ABC的形狀,并求出△ABC的面積;
(3)將拋物線向左或向右平移,得到拋物線L′,L′與x軸相交于A'、B′兩點(點A′在點B′的左側),并與y軸相交于點C′,要使△A'B′C′和△ABC的面積相等,求所有滿足條件的拋物線的函數表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,△ABC是格點三角形(三角形的三個頂點都是小正方形的頂點).
(1)在第一象限內找一點P,以格點P、A、B為頂點的三角形與△ABC相似但不全等,請寫出符合條件格點P的坐標;
(2)請用直尺與圓規在第一象限內找到兩個點M、N,使∠AMB=∠ANB=∠ACB.請保留作圖痕跡,不要求寫畫法.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了落實黨的“精準扶貧”政策,A、B兩城決定向C、D兩鄉運送肥料以支持農村生產,已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉運肥料的費用分別為20元/噸和25元/噸;從B城往C、D兩鄉運肥料的費用分別為15元/噸和24元/噸.現C鄉需要肥料240噸,D鄉需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設從A城運往C鄉肥料x噸,總運費為y元,求出最少總運費.
(3)由于更換車型,使A城運往C鄉的運費每噸減少a(0<a<6)元,這時怎樣調運才能使總運費最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,那么下列判斷不正確的是( )
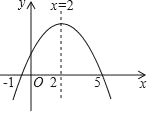
A. ac<0 B. a﹣b+c>0 C. b=﹣4a D. a+b+c>0
查看答案和解析>>
科目:初中數學 來源: 題型:
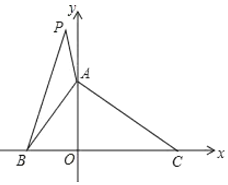
【題目】如圖,已知在平面直角坐標系中,![]() 的面積為8,
的面積為8,![]() ,
,![]() ,點
,點![]() 的坐標是
的坐標是![]() .
.
(1)求![]() 三個頂點
三個頂點![]() 、
、![]() 、
、![]() 的坐標;
的坐標;
(2)若點![]() 坐標為
坐標為![]() ,連接
,連接![]() ,
,![]() ,求
,求![]() 的面積;
的面積;
(3)是否存在點![]() ,使
,使![]() 的面積等于
的面積等于![]() 的面積?如果存在,請求出點
的面積?如果存在,請求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,![]() 中,
中,![]() ,點
,點![]() 是
是![]() 上一點,連接
上一點,連接![]() .
.
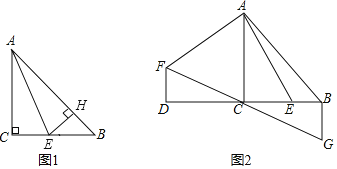
(1)如圖1,當![]() 平分
平分![]() 時,
時,![]() 于
于![]() ,
,![]() 的周長為
的周長為![]() ,求
,求![]() 的長.
的長.
(2)如圖2,延長![]() 至
至![]() ,使
,使![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉90°得線段
順時針旋轉90°得線段![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
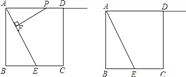
【題目】如圖,正方形 ABCD 的邊長為 4,E 是 BC 的中點,點 P 在射線 AD 上,過點 P 作 PF⊥AE,垂足為 F.
(1)求證:△PFA∽△ABE;
(2)當點 P 在射線 AD 上運動時,設 PA=x,是否存在實數 x,使以 P,F,E 為頂點的三角形也與△ABE
相似?若存在,求出 x 的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com