
【題目】結果如此巧合!
下面是小穎對一道題目的解答.
題目:如圖,Rt△ABC的內切圓與斜邊AB相切于點D,AD=3,BD=4,求△ABC的面積.
解:設△ABC的內切圓分別與AC、BC相切于點E、F,CE的長為x.
根據切線長定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根據勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小穎發現12恰好就是3×4,即△ABC的面積等于AD與BD的積.這僅僅是巧合嗎?
請你幫她完成下面的探索.
已知:△ABC的內切圓與AB相切于點D,AD=m,BD=n.
可以一般化嗎?
(1)若∠C=90°,求證:△ABC的面積等于mn.
倒過來思考呢?
(2)若ACBC=2mn,求證∠C=90°.
改變一下條件……
(3)若∠C=60°,用m、n表示△ABC的面積.

【答案】(1)證明見解析;(2)證明見解析;(3)S△ABC=![]() mn;
mn;
【解析】
(1)設△ABC的內切圓分別與AC、BC相切于點E、F,CE的長為x,仿照例題利用勾股定理得(x+m)2+(x+n)2=(m+n)2,再根據S△ABC=![]() AC×BC,即可證明S△ABC=mn.(2)由ACBC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)過點A作AG⊥BC于點G,在Rt△ACG中,根據條件求出AG、CG,又根據BG=BC-CG得到BG .在Rt△ABG中,根據勾股定理可得x2+(m+n)x=3mn,由此S△ABC=
AC×BC,即可證明S△ABC=mn.(2)由ACBC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)過點A作AG⊥BC于點G,在Rt△ACG中,根據條件求出AG、CG,又根據BG=BC-CG得到BG .在Rt△ABG中,根據勾股定理可得x2+(m+n)x=3mn,由此S△ABC=![]() BCAG=
BCAG=![]() mn.
mn.
設△ABC的內切圓分別與AC、BC相切于點E、F,CE的長為x,
根據切線長定理,得:AE=AD=m、BF=BD=n、CF=CE=x,
(1)如圖1,
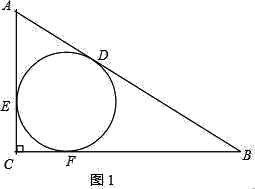
在Rt△ABC中,根據勾股定理,得:(x+m)2+(x+n)2=(m+n)2,
整理,得:x2+(m+n)x=mn,
所以S△ABC=![]() ACBC
ACBC
=![]() (x+m)(x+n)
(x+m)(x+n)
= ![]() [x2+(m+n)x+mn]
[x2+(m+n)x+mn]
=![]() (mn+mn)
(mn+mn)
=mn;
(2)由ACBC=2mn,得:(x+m)(x+n)=2mn,
整理,得:x2+(m+n)x=mn,
∴AC2+BC2=(x+m)2+(x+n)2
=2[x2+(m+n)x]+m2+n2
=2mn+m2+n2
=(m+n)2
=AB2,
根據勾股定理逆定理可得∠C=90°;
(3)如圖2,過點A作AG⊥BC于點G,
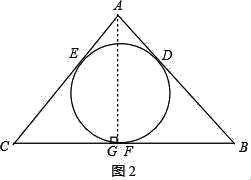
![]() (x+m),CG=ACcos60°=
(x+m),CG=ACcos60°=![]() (x+m),
(x+m),
∴BG=BC﹣CG=(x+n)﹣![]() (x+m),
(x+m),
在Rt△ABG中,根據勾股定理可得:[![]() (x+m)]2+[(x+n)﹣
(x+m)]2+[(x+n)﹣![]() (x+m)]2=(m+n)2,
(x+m)]2=(m+n)2,
整理,得:x2+(m+n)x=3mn,
∴S△ABC=![]() BCAG
BCAG
=![]() ×(x+n)
×(x+n)![]() (x+m)
(x+m)
=![]() [x2+(m+n)x+mn]
[x2+(m+n)x+mn]
=![]() ×(3mn+mn)
×(3mn+mn)
=![]() mn.
mn.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx經過點A(﹣1,![]() )及原點,交x軸于另一點C(2,0),點D(0,m)是y軸正半軸上一動點,直線AD交拋物線于另一點B.
)及原點,交x軸于另一點C(2,0),點D(0,m)是y軸正半軸上一動點,直線AD交拋物線于另一點B.
(1)求拋物線的解析式;
(2)如圖1,連接AO、BO,若△OAB的面積為5,求m的值;
(3)如圖2,作BE⊥x軸于E,連接AC、DE,當D點運動變化時,AC、DE的位置關系是否變化?請證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,將正方形![]() 置于平面直角坐標系中,其中
置于平面直角坐標系中,其中![]() 邊在
邊在![]() 軸上,其余各邊均與坐標軸平行.直線
軸上,其余各邊均與坐標軸平行.直線![]() 沿
沿![]() 軸的負方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形
軸的負方向以每秒1個單位的速度平移,在平移的過程中,該直線被正方形![]() 的邊所截得的線段長為
的邊所截得的線段長為![]() ,平移的時間為
,平移的時間為![]() (秒),
(秒),![]() 與
與![]() 的函數圖象如圖2所示,則圖1中的點
的函數圖象如圖2所示,則圖1中的點![]() 的坐標為__________,圖2中
的坐標為__________,圖2中![]() 的值為__________.
的值為__________.


![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動(
上運動(![]() 不與
不與![]() 、
、![]() 重合),連接
重合),連接![]() ,作
,作![]() ,
,![]() 交線段
交線段![]() 于
于![]() .
.

(1)當![]() 時,
時,![]() ______________
______________![]() ;點
;點![]() 從
從![]() 向
向![]() 運動時,
運動時,![]() 逐漸變____________(填“大”或“小”);
逐漸變____________(填“大”或“小”);
(2)當![]() 時,求證:
時,求證:![]() ,請說明理由;
,請說明理由;
(3)在點![]() 的運動過程中,
的運動過程中,![]() 的形狀也在改變,判斷當
的形狀也在改變,判斷當![]() 等于多少度時,
等于多少度時,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩個一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四個結論中正確的是_____(填寫序號).
①如果方程M有兩個不相等的實數根,那么方程N也有兩個不相等的實數根;
②如果方程M有兩根符號相同,那么方程N的兩根符號也相同;
③如果方程M和方程N有一個相同的根,那么這個根必是x=1;
④如果5是方程M的一個根,那么![]() 是方程N的一個根.
是方程N的一個根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,M為BC上一點,F是AM的中點,EF⊥AM,垂足為F,交AD的延長線于點E,交DC于點N.

(1)求證:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△CAD與△CEB都是等邊三角形,BD、EA的延長線相交于點F.
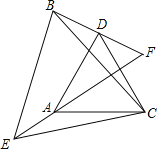
(1)求證:△ACE≌△DCB.
(2)求∠F的度數.
(3)若AD⊥BD,請直接寫出線段EF與線段BD、DF之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】文明交流互鑒是推動人類文明進步和世界和平發展的重要動力.2019年5月“亞洲文明對話大會”在北京成功舉辦,引起了世界人民的極大關注.某市一研究機構為了了解10~60歲年齡段市民對本次大會的關注程度,隨機選取了100名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
組別 | 年齡段 | 頻數(人數) |
第1組 |
| 5 |
第2組 |
|
|
第3組 |
| 35 |
第4組 |
| 20 |
第5組 |
| 15 |

(1)請直接寫出![]() ,
,![]() ,第3組人數在扇形統計圖中所對應的圓心角是 度.
,第3組人數在扇形統計圖中所對應的圓心角是 度.
(2)請補全上面的頻數分布直方圖;
(3)假設該市現有10~60歲的市民300萬人,問40~50歲年齡段的關注本次大會的人數約有多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com