
【題目】在△ABC中,∠ACB=90°,AC=BC,直線,MN經過點C,且AD⊥MN于點D,BE⊥MN于點E。

(1)當直線MN繞點C旋轉到如圖1的位置時,求證:DE=AD+BE;
(2)當直線MN繞點C旋轉到如圖2的位置時,求證:DE=AD-BE;
(3)當直線MN繞點C旋轉到如圖3的位置時,線段DE、AD、BE之間又有什么樣的數量關系?請你寫出這個數量關系,并證明
【答案】(1)證明見詳解;(2)證明見詳解;(3)DE=BE-AD,理由見詳解.
【解析】
(1)利用垂直的定義得∠ADC=∠CEB=90°,則根據互余得∠DAC+∠ACD=90°,再根據等角的余角相等得到∠DAC=∠BCE,然后根據“AAS”可判斷△ADC≌△CEB,所以CD=BE,AD=CE,再利用等量代換得到DE=AD+BE;
(2)與(1)一樣可證明△ADC≌△CEB,則CD=BE,AD=CE,于是有DE=CE-CD=AD-BE;
(3)與(1)一樣可證明△ADC≌△CEB,則CD=BE,AD=CE,于是有DE=CD-CE=BE-AD.
(1)證明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
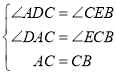 ,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE;
(2)證明:與(1)同理,可證明△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD
證明:與(1)同理,可證明△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CD-CE=BE-AD.


科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,將△ABD沿AB所在的直線折疊,使點D落在點E處;將△ACD沿AC所在的直線折疊,使點D落在點F處,分別延長EB、FC使其交于點M.
(1)判斷四邊形AEMF的形狀,并給予證明.
(2)設AD=x,利用勾股定理,建立關于x的方程模型,求四邊形AEMF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知線段![]() 和線段
和線段![]() .
.

(1)按要求作圖(保留作圍痕跡,不寫作法);
延長線段![]() 至點
至點![]() ,使
,使![]() ,反向延長線段
,反向延長線段![]() 至點
至點![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點,且
的中點,且![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車間接到一批限期(可以提前)完成的零件加工任務.如果每天加工150個,則恰好按期完成;如果每天加工200個,則可比原計劃提前5天完成.
(1)求這批零件的個數;
(2)車間按每天加工200個零件的速度加工了![]() 個零件后,提高了加工速度,每天加工250個零件,結果比原計劃提前6天完成了生產任務,求
個零件后,提高了加工速度,每天加工250個零件,結果比原計劃提前6天完成了生產任務,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”.為保護生態環境,A、B兩村準備各自清理所屬區域養魚網箱和捕魚網箱,每村參加清理人數及總開支如下表:

(1)若兩村清理同類漁具的人均支出費用一樣,求清理養魚網箱和捕魚網箱的人均支出費用各是多少元?
(2)在人均支出費用不變的情況下,為節約開支,兩村準備協調40人共同清理養魚網箱和捕魚網箱.要使總支出不超過102000元,且清理養魚網箱人數小于清理捕魚網箱人數,則有哪幾種分配清理人員方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 經過
經過![]() 頂點
頂點![]() 的一條直線,
的一條直線,![]() .
.![]() 分別是直線
分別是直線![]() 上兩點,且
上兩點,且![]() .
.
(1)若直線![]() 經過
經過![]() 的內部,且
的內部,且![]() 在射線
在射線![]() 上,請解決下面兩個問題:
上,請解決下面兩個問題:
①如圖1,若![]() ,
,![]() ,
,
則![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如圖2,若![]() ,請添加一個關于
,請添加一個關于![]() 與
與![]() 關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
(2)如圖3,若直線![]() 經過
經過![]() 的外部,
的外部,![]() ,請提出
,請提出![]() 三條線段數量關系的合理猜想(不要求證明).
三條線段數量關系的合理猜想(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() ,
,![]() ,且點
,且點![]() 的坐標為
的坐標為![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
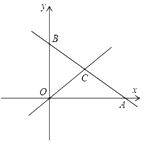
(1)點![]() 的坐標是________,點
的坐標是________,點![]() 的坐標是________;
的坐標是________;
(2)直線![]() 上有一點
上有一點![]() ,若
,若![]() ,試求出點
,試求出點![]() 的坐標;
的坐標;
(3)若點![]() 為直線
為直線![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的垂線,與直線
軸的垂線,與直線![]() 交于點
交于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,線段
,線段![]() 的長度為
的長度為![]() ,求
,求![]() 與
與![]() 的函數解析式.
的函數解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com