
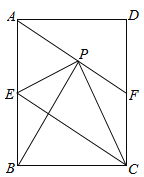
【題目】如圖,在矩形ABCD中,E是AB邊的中點,沿EC對折矩形ABCD,使B點落在點P處,折痕為EC,連結AP并延長AP交CD于F點,
(1)求證:四邊形AECF為平行四邊形;
(2)若△AEP是等邊三角形,連結BP,求證:△APB≌△EPC;
(3)若矩形ABCD的邊AB=6,BC=4,求△CPF的面積.
【答案】(1)證明見試題解析;(2)證明見試題解析;(3)![]() .
.
【解析】
試題分析:(1)由折疊的性質得到BE=PE,EC⊥PB,根據E為AB中點,得到AE=PE,利用等角對等邊得到兩對角相等,利用外角性質得到∠AEP=2∠EPB,設∠EPB=x,則∠AEP=2x,表示出∠APE,由∠APE+∠EPB得到∠APB為90°,進而得到AF與EC平行,再由AE與FC平行,利用兩對邊平行的四邊形為平行四邊形即可得證;
(2)根據等邊三角形性質,得到△AEP三條邊相等,三內角相等,再由折疊的性質及鄰補角定義得到一對角相等,根據同角的余角相等得到一對角相等,再由AP=EB,利用AAS即可得證;
(3)過P作PM⊥CD,在Rt△EBC中,利用勾股定理求出EC,利用面積求出BQ,再根據BP=2BQ求出BP,在Rt△ABP中,利用勾股定理求出AP,根據AF-AP求出PF,由PM與AD平行,得到△PMF與△ADF相似,由相似得比例求出PM,再由FC=AE=3,求出△CPF面積即可.
試題解析:(1)由折疊得到BE=PE,EC⊥PB,∵E為AB的中點,∴AE=EB,即AE=PE,∴∠EBP=∠EPB,∠EAP=∠EPA,∵∠AEP為△EBP的外角,∴∠AEP=2∠EPB,設∠EPB=x,則∠AEP=2x,∠APE=![]() =90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四邊形AECF為平行四邊形;
=90°﹣x,∴∠APB=∠APE+∠EPB=x+90°﹣x=90°,即BP⊥AF,∴AF∥EC,∵AE∥FC,∴四邊形AECF為平行四邊形;
(2)∵△AEP為等邊三角形,∴∠BAP=∠AEP=60°,AP=AE=EP=EB,∵∠PEC=∠BEC,∴∠PEC=∠BEC=60°,∵∠BAP+∠ABP=90°,∠ABP+∠BEQ=90°,∴∠BAP=∠BEQ,在△ABP和△EBC中,∵∠APB=∠EBC=90°,∠BAP=∠BEQ,AP=EB,∴△ABP≌△EBC(AAS),∵△EBC≌△EPC,∴△ABP≌△EPC;
(3)過P作PM⊥DC,交DC于點M,在Rt△EBC中,EB=3,BC=4,根據勾股定理得:EC=![]() =5,∵S△EBC=
=5,∵S△EBC=![]() EBBC=
EBBC=![]() ECBQ,∴BQ=
ECBQ,∴BQ=![]() =
=![]() ,由折疊得:BP=2BQ=
,由折疊得:BP=2BQ=![]() ,在Rt△ABP中,AB=6,BP=
,在Rt△ABP中,AB=6,BP=![]() ,根據勾股定理得:AP=
,根據勾股定理得:AP=![]() =
=![]() ,∵四邊形AECF為平行四邊形,∴AF=EC=5,FC=AE=3,∴PF=
,∵四邊形AECF為平行四邊形,∴AF=EC=5,FC=AE=3,∴PF=![]() =
=![]() ,∵PM∥AD,∴
,∵PM∥AD,∴![]() ,即
,即 ,解得:PM=
,解得:PM=![]() ,則S△PFC=
,則S△PFC=![]() FCPM=
FCPM=![]() =
=![]() .
.



 全能練考卷系列答案
全能練考卷系列答案 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數學 來源: 題型:
【題目】如圖,把矩形ABCD沿EF翻折,點B恰好落在AD邊的B′處,若AE=2,DE=6,∠EFB=60°,則矩形ABCD的面積是( ) 
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,把△ABC向上平移3個單位長度,再向右平移2個單位長度,得到△A′B′C′.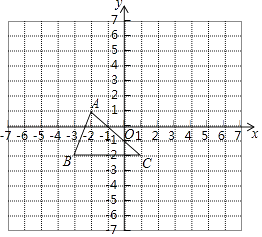
(1)在圖中畫出△A′B′C′;
(2)寫出A′,B′的坐標;
(3)求三角形ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
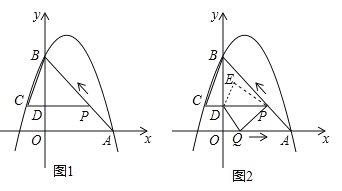
【題目】如圖 1,二次函數![]() 的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
(1)求二次函數![]() 的表達式;
的表達式;
(2)連接 BC ,當t=![]() 時,求△BCP的面積;
時,求△BCP的面積;
(3)如圖 2,動點 P 從 A 出發時,動點 Q 同時從 O 出發,在線段 OA 上沿 O→A 的方向以 1個單位長度的速度運動,當點 P 與 B 重合時,P 、 Q 兩點同時停止運動,連接 DQ 、 PQ ,將△DPQ沿直線 PC 折疊到 △DPE .在運動過程中,設 △DPE 和 △OAB重合部分的面積為 S ,直接寫出 S 與 t 的函數關系式及 t 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】底面半徑為10cm,高為40cm的圓柱形水桶中裝滿了水。小明先將桶中的水倒滿3個底面半徑為3cm,高為5cm的圓柱形杯子,如果剩下的水倒在長、寬、高分別為50cm,20cm和12cm的長方體容器內,會滿出來嗎?若沒有滿出來,求出長方體容器內水的高度( ![]() 取3)。
取3)。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列計算正確的是( )
A.a4+a5=a9B.(2a2b3)2=4a4b6
C.﹣2a(a+3)=﹣2a2+6aD.(a+2b)2=4a2﹣b2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課上,老師提出如下問題:
如圖1,需要在A,B兩地和公路l之間修地下管道,請你設計一種最節省材料的修建方案.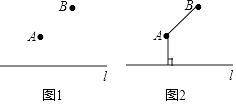
小軍同學的作法如下:
①連接AB;
②過點A作AC⊥直線l于點C;
則折線段B﹣A﹣C為所求.
老師說:小軍同學的方案是正確的.
請回答:該方案最節省材料的依據是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com