
已知△ABC,
(1)如圖l,若P點是 ABC和
ABC和 ACB的角平分線的交點,則
ACB的角平分線的交點,則 P=
P= ;
;
(2)如圖2,若P點是 ABC和外角
ABC和外角 ACE的角平分線的交點,則
ACE的角平分線的交點,則 P=
P=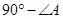 ;
;
(3)如圖3,若P點是外角 CBF和
CBF和 BCE的角平分線的交點,則
BCE的角平分線的交點,則 P=
P=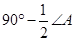 。
。
上述說法正確的個數是( )
| A.0個 | B.1個 | C.2個 | D.3個 |
C
解析該試題考查知識點:三角形的內角和定理、外角、角平分線
思路分析:利用角平分線的定義、三角形的內角和定理進行演算
具體解答過程:
(1)、對圖1來說:
∵P點是 ABC和
ABC和 ACB的角平分線的交點
ACB的角平分線的交點
∴ PBC=
PBC=
 ABC,
ABC, PCB=
PCB=
 ACB
ACB
∵ ABC+
ABC+ ACB=180°-
ACB=180°- A
A
∴ PBC+
PBC+ PCB =
PCB =
 ABC+
ABC+
 ACB=
ACB= (
( ABC+
ABC+ ACB)=
ACB)= (180°-
(180°- A)=90°-
A)=90°-
 A
A
∴ P=180°-(
P=180°-( PBC+
PBC+ PCB)=180°-(90°-
PCB)=180°-(90°-
 A)=
A)=
(2)、對圖2來說:
∵P點是 ABC和外角
ABC和外角 ACE的角平分線的交點
ACE的角平分線的交點
∴ PBC=
PBC=
 ABC,
ABC, PCA=
PCA=
 ACE
ACE
∵ ACE=
ACE= A+
A+ ABC,
ABC, BCA=180°-
BCA=180°- A-
A- ABC
ABC
∴ P=180°-
P=180°- PBC-
PBC- ACB -
ACB - PCA=180°-
PCA=180°-
 ABC-(180°-
ABC-(180°- A-
A- ABC)-
ABC)- (
( A+
A+ ABC)=
ABC)=
 A
A
(3)、對于圖3來說:
∵P點是外角 CBF和
CBF和 BCE的角平分線的交點
BCE的角平分線的交點
∴ PBC=
PBC= ,
, PCB=
PCB=
 P=180°-
P=180°- PBC-
PBC- PCB=180°-
PCB=180°-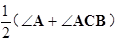 -
- =180°-
=180°- A-
A- (
( ACB+
ACB+ ABC)=180°-
ABC)=180°- A-
A- (180°-
(180°- A)=
A)=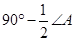
綜上所述,與題中所給的說法對比可知:只有(1)和(3)兩個是正確的。
故選C
試題點評:演算繁瑣,需及時化簡。這類題目在中考中出現的幾率較小,但作為平時的練習還是有一定價值的。


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等邊三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:
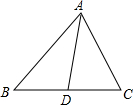 如圖,已知ABC中,AD為BC邊上的中線,且AB=4cm,AC=3cm,則AD的取值范圍是( )
如圖,已知ABC中,AD為BC邊上的中線,且AB=4cm,AC=3cm,則AD的取值范圍是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com