
【題目】如圖,△ABC中,AB=AC,BE⊥AC于E,且D、E分別是AB、AC的中點,延長BC至點F,使CF=CE.
(1)∠ABC的度數.
(2)求證:BE=FE.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC的底邊BC長為4,面積是16,腰AC的垂直平分線EF分別交AC,AB邊于E,F點![]() 若點D為BC邊的中點,點M為線段EF上一動點,則
若點D為BC邊的中點,點M為線段EF上一動點,則![]() 周長的最小值為
周長的最小值為![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A、B均在由面積為1的相同小矩形組成的網格的格點上,建立平面直角坐標系如圖所示.若P是x軸上使得![]() 的值最大的點,Q是y軸上使得QA十QB的值最小的點,則
的值最大的點,Q是y軸上使得QA十QB的值最小的點,則![]() = ▲ .
= ▲ .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,折疊長方形(四個角都是直角)的一邊AD使點D落在BC邊的點F處,已知AB=DC=8cm,AD=BC=10cm,

求:(1)求BF長度;
(2)求CE的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用配方法求出拋物線![]() 的頂點坐標、對稱軸、最大值或最小值;若將拋物線
的頂點坐標、對稱軸、最大值或最小值;若將拋物線![]() 先向左平移
先向左平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,所得拋物線的函數關系式為________.
個單位,所得拋物線的函數關系式為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線一點,點O是線段AD上一點,OP=OC.
(1)已知∠APO=18°,求∠DCO的度數;
(2)求證:△OPC是等邊三角形;
(3)求證:AC=AO+AP.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某人在大樓30米高(即PH=30米)的窗口P處進行觀測,測得山坡上A處的俯角為15°,山腳B處的俯角為60°,已知該山坡的坡度i為1∶![]() ,點P,H,B,C,A在同一個平面上,點H,B,C在同一條直線上,且PH⊥HC.則A,B兩點間的距離是( )
,點P,H,B,C,A在同一個平面上,點H,B,C在同一條直線上,且PH⊥HC.則A,B兩點間的距離是( )
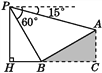
A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
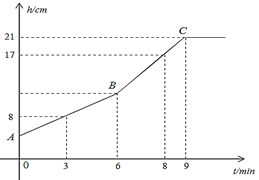
【題目】某興趣小組觀察下雨天學校池塘水面高度h(單位:cm)與觀察時間t(單位:min)的關系,并根據當天觀察數據畫出了如圖所示的圖象,請你結合圖象回答下列問題:
(1)求線段BC的表達式;
(2)試求出池塘原有水面的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點P是CD邊上一動點,連接PA,分別過點B、D作BE⊥PA、DF⊥PA,垂足分別為E、F,如圖①。
(1)請探究BE、DF、EF這三條線段的長度具有怎樣的數量關系?并說明理由。
(2)若點P在DC的延長線上,如圖②,那么這三條線段的長度之間又具有怎樣的數量關系?直接寫出結論。
(3)若點P在CD的延長線上呢,如圖③,直接寫出結論。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com