
���}Ŀ����D��һ�Һ�݆λ�ڟ���P����ƫ�|60�����x����100�����A̎����Ӌ��ȥ��λ�ڟ���P�ı�ƫ�|45�����ϵ�B̎.��������(sh��)��(j��)![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732�� ![]() ��2.449��
��2.449��
��1����B̎���x����P�ж��h�����Y(ji��)�����_��0.1���
��2�����O(sh��)��һ�A�ΰ����^(q��)�����ĈA��λ���侀PB�ϣ����x����190������cO̎.�A�ΰ����^(q��)��İ돽��50����M���@���^(q��)�����|����Σ�U.Ո�Дຣ݆���_B̎�Ƿ����|����Σ�U�����f������.

���𰸡���1��B̎���xP��122.5���2���]��Σ�U
��������ԇ�}��������1�����ȸ���(j��)�}��ó���MPA=��PAD=60�����Լ���PDB=��PBD=45���������ý�ֱ��������������ɣ���2���������OB���L���M���ó�OB��50�����ɵó��𰸣�
ԇ�}������
(1)��PC��AB���cC
��Rt��PAC����PCA=90����CPA=90-60=30
��PC=PA��cos30=![]()
��Rt��PCB����PCB=90����PBC=90-45=45
��PB=![]() PC=
PC=![]() ��122.5
��122.5
��B̎���xP��122.5����.
��2���]���U.
�������£�
OB=OP-PB=![]()
![]() =
=![]()
![]() ��
��
��OB>50�����o�U



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��������![]() �У��c
���c![]() ��
��![]() �քe�ھ���
�քe�ھ���![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ���c
���c![]() ��ֱ��
��ֱ��![]() ���\�ӣ�
���\�ӣ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ���^�c
���^�c![]() ��
��![]() ����ֱ��
����ֱ��![]() ��
��![]() ��
��

��1����D1����(d��ng)�c![]() �ھ���
�ھ���![]() �����L���ϕr�����C��
�����L���ϕr�����C��![]() ��
��
��2����D2����(d��ng)�c![]() �ھ���
�ھ���![]() �����L���ϕr�����D�a���������c
�����L���ϕr�����D�a���������c![]() �ھ���
�ھ���![]() �ϣ��B��
�ϣ��B��![]() ����
����![]() �����C��
�����C��![]() ��
��
��3���ڣ�2���ėl���£����L![]() ���c
���c![]() �����L
�����L![]() ���c
���c![]() ����
����![]() ��
��![]() ���t
���t![]() �ĶȔ�(sh��)��������ֱ�ӌ����Y(ji��)������
�ĶȔ�(sh��)��������ֱ�ӌ����Y(ji��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����x���в���:
���}����D1����ƽ����߅��ABCD��,E��AD��һ�c��AE=AB����EAB=60�����^�cE��ֱ��EF����EF��ȡһ�cG.ʹ�á�EGB=��EAB,�B��AG.
���C:EG=AG+BG.


С��ͬ�W(xu��)��˼·��:����CAM=��EAB��CE���cH����(g��u)��ȫ�������Σ���(j��ng)�^������Q���}.
����С��ͬ�W(xu��)��˼·��̽������Q���І��}:
(1)������憖�}�е��C����
(2)�����ԭ���}�еġ���EAB=60�㡱�Ğ顰��EAB=90�㡱��ԭ���}�е������l����׃(��D2),Ո?zh��)�������EC��AG��BG֮�g�Ĕ�(sh��)���P(gu��n)ϵ,���C����ĽY(ji��)Փ.
��:����EG��AG��BG֮�g�Ĕ�(sh��)���P(gu��n)ϵ��___________________________________________________.�C��:
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���Ҳ��ŵă��w���ĸ߶ȷքe��AB=8�ף�CD=12�ף��ɘ��ˮƽ���xBD=5�ף�һ�^�y�ߵ��۾���EF=1.6�ף���E��B��D��һ�lֱ���ϣ���(d��ng)�^�y�ߵ�ҕ��FACǡ�ý�(j��ng)�^�ɿØ��픶˕r����߅��ABDC�ą^(q��)�����^�y�ߵ�ä�^(q��)���t�˕r�^�y���c��AB�ľ��xEB���ڣ�������

A��8�� B��7�� C��6�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D1�����タy=-![]() x2+bx+c�cx�S�ཻ���cA��C���cy�S�ཻ���cB���B��AB��BC���cA������(bi��o)����2��0����tan��BAO=2���Ծ���BC��ֱ������M��AB���cD���^�cB��ֱ��l��AC���c���タ����M����һ�����c�քe��E��F(xi��n)��
x2+bx+c�cx�S�ཻ���cA��C���cy�S�ཻ���cB���B��AB��BC���cA������(bi��o)����2��0����tan��BAO=2���Ծ���BC��ֱ������M��AB���cD���^�cB��ֱ��l��AC���c���タ����M����һ�����c�քe��E��F(xi��n)��

��1����ԓ���タ�ĺ���(sh��)���_ʽ��
��2�����cC������(bi��o)�;���EF���L��
��3����D2���B��CD�����L����ֱ��l���cN���cP��Q���侀NB�ϵăɂ����c���cP���cQ���҂�(c��)���Ҳ��cN�غ���������PQ�cEF���L����ȣ��B��DP��CQ����߅��CDPQ�����L�Ƿ�����Сֵ�����У�Ո����˕r�cP������(bi��o)��ֱ�ӌ�����߅��CDPQ���L����Сֵ�����]�У�Ո�f��������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����һ�����ǰ��еăɉKֱ�����ǰ��ֱ����c![]() ����D��ʽ�B����һ��������ʾ��
����D��ʽ�B����һ��������ʾ��![]() ��
��![]() ��
��![]() .
.
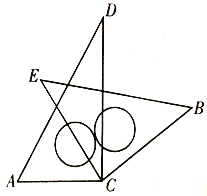
��1������![]() ���t
���t![]() �ĶȔ�(sh��)��__________��
�ĶȔ�(sh��)��__________��
����![]() ���t
���t![]() �ĶȔ�(sh��)��__________.
�ĶȔ�(sh��)��__________.
��2���ɣ�1������![]() �c
�c![]() �Ĕ�(sh��)���P(gu��n)ϵ�����f�����ɣ�
�Ĕ�(sh��)���P(gu��n)ϵ�����f�����ɣ�
��3����(d��ng)![]() ���c
���c![]() ��ֱ��
��ֱ��![]() ���Ϸ��r����(d��ng)�@�ɉK�dz���һ�M߅����ƽ�Еr��Ոֱ�ӌ���
���Ϸ��r����(d��ng)�@�ɉK�dz���һ�M߅����ƽ�Еr��Ոֱ�ӌ���![]() �Ƕ����п��ܵ�ֵ.
�Ƕ����п��ܵ�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
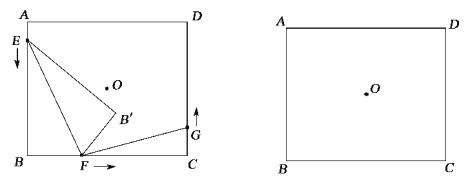
���}Ŀ����D���cO�����ABCD�Č��Q���ģ�AB��10cm��BC��12cm���cE��F��G�քe��A��B��C���cͬ�r���l(f��)���ؾ��ε�߅����rᘷ�������\�ӣ��cE���\���ٶȞ�1cm/s���cF���\���ٶȞ�3cm/s���cG���\���ٶȞ�xcm/s����(d��ng)�cF���_�cC�����cF�c�cC�غϣ��r�������c�Sֹ֮ͣ�\�ӣ����\���^���У���EBF�P(gu��n)��ֱ��EF�Č��Q�D���ǡ�EB'F���O(sh��)�cE��F��G�\�ӵĕr�g��t����λ��s����
��1����(d��ng)t�� s�r����߅��EBFB'�������Σ�
��2����(d��ng)x���ֵ�r�����cE��B��F����c���������c���cF��C��G����c�������ο���ȫ�ȣ�
��3���Ƿ���ڌ���(sh��)t��ʹ���cB'�c�cO�غϣ������ڣ����t��ֵ���������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������f�������_�Ă���(sh��)�ǣ� ��
�ك��c֮�g�������B���У�������̣�����ȵĽ��nj�픽ǣ����^һ�c���҃H��һ�lֱ���c��ֱ֪��ƽ�У��܃��c֮�g�ľ��x�ǃ��c�g�ľ��Σ�����![]() ���t�c
���t�c![]() �龀��
�龀��![]() �����c�����ཻ�ăɗlֱ������ƽ�о���
�����c�����ཻ�ăɗlֱ������ƽ�о���
A. ![]() ��B.
��B. ![]() ��C.
��C. ![]() ��D.
��D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
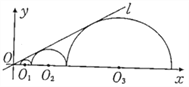
���}Ŀ����D���A�Ķ���x�S�����S�ϵİ�AO1����AO2��������AOn���cֱ��l���У��O(sh��)��AO1����AO2��������AOn�İ돽�քe��r1��r2������rn���t��(d��ng)ֱ��l�cx�S�����J�Ǟ�30![]() �r����r1=1�r��r2017=_______.
�r����r1=1�r��r2017=_______.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com