
【題目】如圖,直線y=kx+4(k≠0)與x軸、y軸分別交于點B,A,直線y=-2x+1與y軸交于點C,與直線y=kx+4交于點D,△ACD的面積是![]() .
.
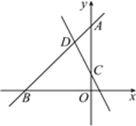
(1)求直線AB的表達式;
(2)設點E在直線AB上,當△ACE是直角三角形時,求出點E的坐標.
【答案】(1)y=x+4;(2)點E的坐標為(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).
【解析】
(1)將x=0分別代入兩個一次函數(shù)表達式中求出點A、C的坐標,進而即可得出AC的長度,再根據(jù)三角形的面積公式結(jié)合△ACD的面積即可求出點D的橫坐標,利用一次函數(shù)圖象上點的坐標特即可求出點D的坐標,由點D的坐標利用待定系數(shù)法即可求出直線AB的表達式;
(2)由直線AB的表達式即可得出△ACE為等腰直角三角形,分∠ACE=90°和∠AEC=90°兩種情況考慮,根據(jù)點A、C的坐標利用等腰直角三角形的性質(zhì)即可得出點E的坐標,此題得解.
解:(1)當x=0時,y=kx+4=4,y=-2x+1=1,
∴A(0,4),C(0,1),
∴AC=3.
∵S△ACD=![]() ,
,
∴![]() ,
,
∵點D在第二象限,
點D的橫坐標為![]() .
.
當x=![]() 時,y=
時,y=![]() 2x+1=3,
2x+1=3,
∴D(![]() 1,3).
1,3).
將D(![]() 1,3)代入y=kx+4,
1,3)代入y=kx+4,
![]() k+4=3,解得:k=1.
k+4=3,解得:k=1.
∴直線AB的表達式為:y=x+4.
(2)∵直線AB的表達式為y=x+4,
∴△ACE為等腰直角三角形.
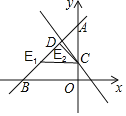
當∠ACE=90°時,∵A(0,4),C(0,1),AC=3,
∴E1(![]() 3,1);
3,1);
當∠AEC=90°時,∵A(0,4),C(0,1),AC=3,
∴E2(![]()
![]() ,
,![]() ).
).
綜上所述:當△ACE是直角三角形時,點E的坐標為(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).


 口算能手系列答案
口算能手系列答案科目:初中數(shù)學 來源: 題型:
【題目】如果一元二次方程ax2+bx+c=0(a≠0)的兩根是x1、x2,那么利用公式法寫出兩個根x1、x2,通過計算可以得出:x1+x2=![]() ,x1x2=
,x1x2=![]() .由此可見,一元二次方程兩個根的和與積是由方程的系數(shù)決定的.這就是一元二次方程根與系數(shù)的關(guān)系.
.由此可見,一元二次方程兩個根的和與積是由方程的系數(shù)決定的.這就是一元二次方程根與系數(shù)的關(guān)系.
請利用上述知識解決下列問題:
(1)若方程2x2-4x-1=0的兩根是x1、x2,則x1+x2=__________,x1x2=__________.
(2)已知方程x2-4x+c=0的一個根是![]() ,請求出該方程的另一個根和c的值.
,請求出該方程的另一個根和c的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某彈簧掛上不超過20千克的物體后按一定規(guī)律伸長,測得一彈簧的長度![]() (厘米)與所掛的物體的質(zhì)量
(厘米)與所掛的物體的質(zhì)量![]() (千克)有下面的關(guān)系:
(千克)有下面的關(guān)系:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
那么彈簧的總長![]() (厘米)與所掛的物體的質(zhì)量
(厘米)與所掛的物體的質(zhì)量![]() (千克)之間是否是函數(shù)關(guān)系?若是,請寫出函數(shù)關(guān)系式.
(千克)之間是否是函數(shù)關(guān)系?若是,請寫出函數(shù)關(guān)系式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】 端午節(jié)期間,小明一家自駕游去了離家200![]() 的某地,如下圖是他們離家的距離
的某地,如下圖是他們離家的距離![]() 與汽車行駛時間
與汽車行駛時間![]() 之間的函數(shù)圖象. 根據(jù)圖象解答下列問題:
之間的函數(shù)圖象. 根據(jù)圖象解答下列問題:
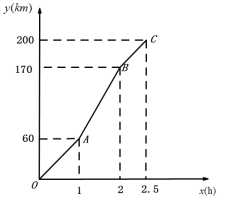
(1)點![]() 的實際意義;
的實際意義;
(2)求出線段![]() 的函數(shù)表達式;
的函數(shù)表達式;
(3)他們出發(fā)2.3![]() 時,距目的地還有多少
時,距目的地還有多少![]() ?
?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖Rt△ABC中∠ACB=90°,將其折疊使點A落在邊BC的點A′處,折痕為CD,若∠A′DB=20°,則∠B=( )
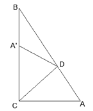
A.45°B.35°C.30°D.40°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】冬至過后,晝夜溫差逐漸加大,山城的市民們已然感受到了深冬的寒意.在還未普遍使用地暖供暖設備的山城,小型電取暖器仍然深受市民的青睞.某格力專賣店銷售壁掛式電暖器和鹵素/石英式取暖器(俗稱 “小太陽”),其中壁掛式電暖器的售價是“小太陽”售價的5倍還多100元,2016年12月份壁掛式電暖器和“小太陽”共銷售500臺,壁掛式電暖器與“小太陽”銷量之比是4∶1,銷售總收入為58.6萬元.
(1)分別求出每臺壁掛式電暖器和“小太陽”的售價;
(2)隨著“元旦、春節(jié)”雙節(jié)的來臨和氣溫的回升,銷售進入淡季,2017年1月份,壁掛式電暖器的售價比2016年12月下調(diào)了4m﹪,根據(jù)經(jīng)驗銷售量將比2016年12月下滑6m﹪,而“小太陽”的銷售量和售價都維持不變,預計銷售總收入將下降到16.04萬元,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】對于平面直角坐標系xOy中的點![]() ,若點Р的坐標為
,若點Р的坐標為![]() (其中k為常數(shù),且
(其中k為常數(shù),且![]() ),則稱點
),則稱點![]() 為點P的“k屬派生點”.
為點P的“k屬派生點”.
例如:![]() 的“2屬派生點”為
的“2屬派生點”為![]() ,即
,即![]() .
.
(1)點![]() 的“3屬派生點”
的“3屬派生點”![]() 的坐標為________;
的坐標為________;
(2)若點![]() 的“5屬派生點”
的“5屬派生點” ![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值;
的值;
(3)若點P在x軸的正半軸上,點Р的“k屬派生點”為點![]() ,且線段
,且線段![]() 的長座為線段OP長度的2倍,求k的值.
的長座為線段OP長度的2倍,求k的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
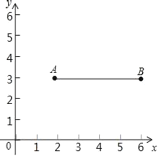
【題目】在平面直角坐標系中,已知點A(2,3),B(6,3),連接AB,如果點P在直線y=x﹣1上,且點P到直線AB的距離小于1,那么稱點P是線段AB的“臨近點”,則下列點為AB的“臨近點”的是( )
A.(![]() ,
,![]() )B.(3,3)C.(6,5)D.(1,0)
)B.(3,3)C.(6,5)D.(1,0)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com