
【題目】某莊有甲、乙兩家草莓采摘園的草莓銷售價格相同,春節期間,兩家采摘園將推出優惠方案,甲園的優惠方案是:游客進園需購買門票,采摘的草莓六折優惠;乙園的優惠方案是:游客進園不需購買門票,采摘的草莓超過一定數量后,超過部分打折優惠.優惠期間,某游客的草莓采摘量為![]() (千克),在甲園所需總費用為
(千克),在甲園所需總費用為![]() (元),在乙園所需總費用為
(元),在乙園所需總費用為![]() (元),
(元),![]() 、
、![]() 與
與![]() 之間的函數關系如圖所示.
之間的函數關系如圖所示.

(1)甲采摘園的門票是_____元,兩個采摘園優惠前的草莓單價是每千克____元;
(2)當![]() 時,求
時,求![]() 與
與![]() 的函數表達式;
的函數表達式;
(3)游客在“春節期間”采摘多少千克草莓時,甲、乙兩家采摘園的總費用相同.
【答案】(1)60,30;(2)![]() ;(3)采摘5千克或20千克草莓時,甲、乙兩家采摘園的總費用相同.
;(3)采摘5千克或20千克草莓時,甲、乙兩家采摘園的總費用相同.
【解析】
(1)根據單價=總價÷數量,即可解決問題;
(2)y乙與x的函數表達式結合圖象利用待定系數法即可解決.
(3)根據圖象可得y甲函數表達式,分別討論x<10和x>10時,y甲=y乙,求出x的值即可.
(1)由圖象可知:甲采摘園的門票是60元,
由y乙圖象可知采摘草莓10千克的費用為300元,且超過10千克打折,
∴優惠前的草莓單價是每千克300÷10=30元,
故答案為:60,30;
(2)當![]() 時,設
時,設![]()
把點![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴當![]() 時,
時,![]() ,
,
(3)![]()
當![]() 時,
時,![]()
![]() ,解得
,解得![]()
當![]() 時,
時,![]()
解得![]()
∴采摘5千克或20千克草莓時,甲、乙兩家采摘園的總費用相同.


科目:初中數學 來源: 題型:
【題目】已知某項工程由甲、乙兩隊合做12天可以完成,共需工程費用27720元.乙隊單獨完成這項工程所需時間是甲隊單獨完成這項工程所需時間的1.5倍,且甲隊每天的工程費用比乙隊多250元.
(1)求甲、乙兩隊單獨完成這項工程各需多少天?
(2)若工程管理部門決定從這兩個隊中選一個隊單獨完成此項工程,從節約資金的角度考慮,應選擇哪個工程隊?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E,F分別在邊CD,BC上,且∠EAF=45°,BD分別交AE,AF于點M,N,以點A為圓心,AB長為半徑畫弧BD.下列結論:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④ ![]() 與EF相切;⑤EF∥MN.其中正確結論的個數是( )
與EF相切;⑤EF∥MN.其中正確結論的個數是( )
A.5個
B.4個
C.3個
D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是△ABC的角平分線,點E,F分別在BC,AB上,且DE∥AB,BE=AF.
(1)求證:四邊形ADEF是平行四邊形;
(2)若∠ABC=60°,BD=4,求平行四邊形ADEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=a(x﹣m)2﹣a(x﹣m)(a,m為常數,且a≠0).
(1)求證:不論a與m為何值,該函數的圖象與x軸總有兩個公共點;
(2)設該函數的圖象與x軸的兩個交點為A(x1 , 0),B(x2 , 0),且x12+x22=25,求m的值;
(3)設該函數的圖象的頂點為C,與x軸交于A,B兩點,且△ABC的面積為1,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】旋轉變換是解決數學問題中一種重要的思想方法,通過旋轉變換可以將分散的條件集中到一起,從而方便解決問題.已知,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 在邊
在邊![]() 上,且
上,且![]() .
.

(1)如圖![]() ,當
,當![]() 時,將
時,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 到
到![]() 的位置,連接
的位置,連接![]() ,
,
①求![]() 的度數;
的度數;
②求證:![]() ;
;
(2)如圖![]() ,當
,當![]() 時,猜想
時,猜想![]() 、
、![]() 、
、![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
(3)如圖![]() ,當
,當![]() ,
,![]() ,
,![]() 時,請直接寫出
時,請直接寫出![]() 的長為________.
的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形AB1C1D1的邊長為1,∠B1=60°;作AD2⊥B1C1于點D2 , 以AD2為一邊,做第二個菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于點D3 , 以AD3為一邊做第三個菱形AB3C3D3 , 使∠B3=60°…依此類推,這樣做的第n個菱形ABnCnDn的邊ADn的長是 . 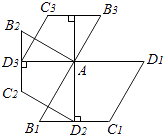
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請你補全證明過程:如圖,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求證:EF∥CD

證明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解決下列問題:
材料一:對非負實數x“四舍五入”到個位的值記為![]() ,即:當n為非負整數時,如果
,即:當n為非負整數時,如果![]() ,則
,則![]() ;反之,當n為非負整數時,如果
;反之,當n為非負整數時,如果![]() ;則
;則![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐標系中任意兩點![]() ,
,![]() ,我們把
,我們把![]() 叫做
叫做![]() 、
、![]() 兩點間的折線距離,并規定
兩點間的折線距離,并規定![]() 若
若![]() 是一定點,
是一定點,![]() 是直線
是直線![]() 上的一動點,我們把
上的一動點,我們把![]() 的最小值叫做
的最小值叫做![]() 到直線
到直線![]() 的折線距離,例如:若
的折線距離,例如:若![]() ,
,![]() 則
則![]() .
.
![]() 如果
如果![]() ,寫出實數x的取值范圍;
,寫出實數x的取值范圍;![]() 已知點
已知點![]() ,點
,點![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m為滿足
若m為滿足![]() 的最大值,求點
的最大值,求點![]() 到直線
到直線![]() 的折線距離.
的折線距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com