
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 旋轉,邊
旋轉,邊![]() 分別交邊
分別交邊![]() 、
、![]() 于
于![]() 、
、![]() 兩點.
兩點.
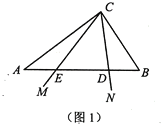

(1)若![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)如圖2,設![]() ,點
,點![]() 是
是![]() 的中點,連接
的中點,連接![]() ,當
,當![]() 旋轉到
旋轉到![]() 與
與![]() 的交點
的交點![]() 是
是![]() 的中點時,過點
的中點時,過點![]() 作
作![]() 的垂線交CM于點
的垂線交CM于點![]() ,連接
,連接![]() 、
、![]() ,求證:
,求證:![]() .
.
科目:初中數學 來源: 題型:
【題目】現有兩組相同的撲克牌,每組兩張,兩張牌的牌面數字分別是2和3,從每組牌中各隨機摸出一張牌,稱為一次試驗.
(1)小紅與小明用一次試驗做游戲,如果摸到的牌面數字相同小紅獲勝,否則小明獲勝,請用列表法或畫樹狀圖的方法說明這個游戲是否公平?
(2)小麗認為:“在一次試驗中,兩張牌的牌面數字和可能為4、5、6三種情況,所以出現‘和為4’的概率是![]() ”,她的這種看法是否正確?說明理由.
”,她的這種看法是否正確?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 是第一、三象限的角平分線.
是第一、三象限的角平分線.

(1)由圖觀察易知A(0,2)關于直線l的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(-2,5)關于直線l的對稱點B′、C′的位置,并寫出他們的坐標:![]() ___________、
___________、![]() ___________;
___________;
(2)結合圖形觀察以上三組點的坐標,你會發現:坐標平面內任一點![]() 關于第一、三象限的角平分線
關于第一、三象限的角平分線![]() 的對稱點
的對稱點![]() 的坐標為___________(不必證明);
的坐標為___________(不必證明);
(3)已知兩點![]() 、
、![]() ,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
,試在直線L上畫出點Q,使點Q到D、E兩點的距離之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
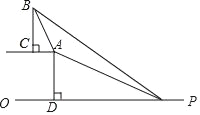
【題目】已知,如圖,在坡頂A處的同一水平面上有一座大型紀念碑BC,某同學在斜坡底P處測得該碑的碑頂B的仰角為45°,然后他們沿著坡度為1:2.4的斜坡AP攀行了26米到達坡頂A,在坡頂A處又測得該碑的碑頂B的仰角為76°,求紀念碑BC的高度(結果精確到0.1米).(過點A作AD⊥PO,垂足為點D.坡度=AD:PD)(參考數據:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司試銷一種成本單價為50元/件的新產品,規定試銷時銷售單價不低于成本單價,又不高于80元/件,經試銷調查,發現銷售量y(件)與銷售單價x(元/件)可近似看作一次函數y=kx+b的關系(如圖所示)
(I)根據圖象,求一次函數y=kx+b的解析式,并寫出自變量x的取值范圍;
(Ⅱ)該公司要想每天獲得最大的利潤,應把銷售單價定為多少?最大利潤值為多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() 交于A、B兩點,且點A的橫坐標為
交于A、B兩點,且點A的橫坐標為![]() .
.
(1)求k的值;
(2)若雙曲線y=![]() 上點C的縱坐標為3,求△AOC的面積;
上點C的縱坐標為3,求△AOC的面積;
(3)在坐標軸上有一點M,在直線AB上有一點P,在雙曲線y=![]() 上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.
上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,在下列代數式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正確的個數為( )
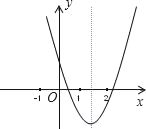
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1解析式為y=x+2,且與坐標軸分別交于A、B兩點,與雙曲線交于點P(﹣1,1).點M是雙曲線在第四象限上的一點,過點M的直線l2與雙曲線只有一個公共點,并與坐標軸分別交于點C、點D,當四邊形ABCD的面積取最小值時,則點M的坐標為( )
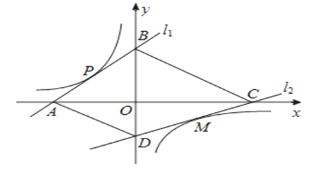
A. (1,﹣1) B. (2,﹣![]() ) C. (3,﹣
) C. (3,﹣![]() ) D. 不能確定
) D. 不能確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com