
【題目】如圖,拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() ,且點
,且點![]() 與點
與點![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,點
,點![]() 是拋物線的頂點.
是拋物線的頂點.

(1)求二次函數的關系式.
(2)點![]() 為線段
為線段![]() 上一個動點,過點
上一個動點,過點![]() 作
作![]() 軸于點
軸于點![]() .若
.若![]() ,
,![]() 的面積為
的面積為![]() .
.
①求![]() 與
與![]() 的函數關系式,寫出自變量
的函數關系式,寫出自變量![]() 的取值范圍.
的取值范圍.
②當![]() 取得最值時,求點
取得最值時,求點![]() 的坐標.
的坐標.
(3)在![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為直角三角形?如果存在,請直接寫出點
為直角三角形?如果存在,請直接寫出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ;②P(
;②P(![]() ,3);
,3);
(3)![]() 或
或![]()
【解析】
(1)將點B、C的坐標代入![]() 即可;
即可;
(2)①求出頂點坐標,直線MB的解析式等,由PD⊥x軸且OD=m知P(m,-2m+6),即可用含m的代數式表示出S;
②在和①的情況下,將S和m的關系式化為頂點式,由二次函數的圖象和性質即可寫出點P的坐標;
(3)分情況討論,當∠CPD=90°時,推出PD=CO=3,則點P的縱坐標為3,即可求出點P的坐標;當∠PCD=90°時,證∠PDC=∠OCD,由銳角三角函數可求出m的值,即可寫出點P的坐標;當∠PDC=90°時,不存在點P.
解:(1)將![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴二次函數的解析式為![]() ;
;
(2)①∵![]()
∴頂點M(1,4),
將直線BM的解析式設為![]() ,
,
將點![]() ,M(1,4)代入,
,M(1,4)代入,
可得![]() ,
,
解得![]() ,
,
∴直線BM的解析式為![]() ,
,
如圖∵PD⊥x軸且OD=m,
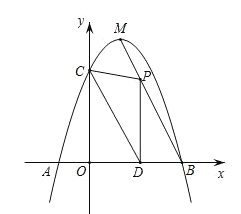
∴P(m,-2m+6),
∴![]() ,
,
即![]() ,
,
∵點![]() 為線段
為線段![]() 上一個動點且
上一個動點且![]() ,M(1,4),
,M(1,4),
∴![]() ;
;
②![]() ,
,
∴當![]() 時,S取最大值
時,S取最大值![]() ,
,
∴P(![]() ,3);
,3);
(3)存在,理由如下:
如圖,當∠CPD=90°時,
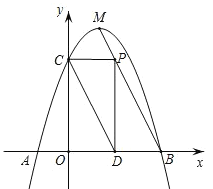
![]() ,
,
∴四邊形CODP為矩形,
∵PD=CO=3,
將![]() 代入直線
代入直線![]() ,
,
得![]() ,
,
∴P![]() ;
;
如圖,當∠PCD=90°時,

∵OC=3,OD=m,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴![]() ;
;
當∠PDC=90°時,
∵PD⊥x軸,
∴不存在點P;
綜上所述,點P的坐標為![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源.某城市環保部門為了提高宣傳實效,抽樣調查了部分居民小區一段時間內生活垃圾的分類情況,其相關信息如下:

根據圖表解答下列問題:
(1)請將條形統計圖補充完整;
(2)在扇形統計圖樣中,產生的有害垃圾C所對應的圓心角 度;
(3)調查發現,在可回收物中塑料類垃圾占13%,每回收1噸塑料類垃圾可獲得0.5噸二級原料.假設該城市每月產生的生活垃圾為1000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
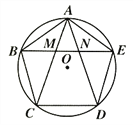
【題目】如圖,正五邊形的邊長為2,連接對角線AD、BE、CE,線段AD分別與BE和CE相交于點M、N,給出下列結論:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正確的結論是_________(把你認為正確結論的序號都填上).
-1,其中正確的結論是_________(把你認為正確結論的序號都填上).
查看答案和解析>>
科目:初中數學 來源: 題型:
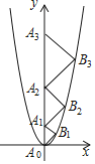
【題目】二次函數![]() 的圖象如圖,點
的圖象如圖,點![]() 位于坐標原點,點
位于坐標原點,點![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函數
在二次函數![]() 位于第一象限的圖象上,
位于第一象限的圖象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角頂點在拋物線上的等腰直角三角形,則
都是直角頂點在拋物線上的等腰直角三角形,則![]() 的斜邊長為________.
的斜邊長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形 ABCD 中,E是BC的中點,F是CD上一點,AE⊥EF.有下列結論:
①∠BAE=30°;
②射線FE是∠AFC的角平分線;
③CF=![]() CD;
CD;
④AF=AB+CF.
其中正確結論的個數為( )
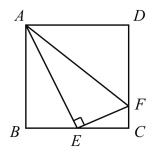
A.1 個B.2 個C.3 個D.4 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人加工同一種零件,甲每天加工的數量是乙每天加工數量的1.5倍,兩人各加工300個這種零件,甲比乙少用5天.
(1)求甲、乙兩人每天各加工多少個這種零件?
(2)已知甲、乙兩人加工這種零件每天的加工費分別是150元和120元,現有1500個這種零件的加工任務,甲單獨加工一段時間后另有安排,剩余任務由乙單獨完成.如果總加工費為7800元,那么甲、乙各加工了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某建筑物的頂部有一塊標識牌 CD,小明在斜坡上 B 處測得標識牌頂部C 的仰角為 45°, 沿斜坡走下來在地面 A 處測得標識牌底部 D 的仰角為 60°,已知斜坡 AB 的坡角為 30°,AB=AE=10 米.則標識牌 CD 的高度是( )米.
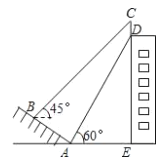
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中數學 來源: 題型:
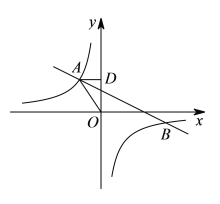
【題目】如圖,在平面直角坐標系中,反比例函數![]()
![]() 與一次函數
與一次函數![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
(1)求反比例函數和一次函數的解析式;
(2)請根據圖象直接寫出![]() 的自變量
的自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com