
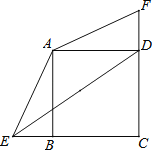
【題目】在正方形ABCD中,BC=2,E、F分別是CB、CD延長線上的點,DF=BE,連接AE、AF.
(1)求證:△ADF≌△ABE.
(2)若BE=1,求sin∠AED的值.
【答案】(1)見解析; (2) ![]()
【解析】
(1)根據正方形的性質可得AB=DA,∠ABE=∠ADF=90°,再根據DF=BE,即可證明△ADF≌△ABE(SAS).
(2)作AH⊥DE于H,由勾股定理得DE=![]() ,AE=
,AE=![]() ,根據三角形面積公式求出AH=
,根據三角形面積公式求出AH=![]() ,即可求出sin∠AED的值.
,即可求出sin∠AED的值.
解:(1)∵四邊形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠ABE=∠ADF=90°,
在△ADF和△ABE中:
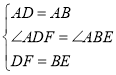
∴△ADF≌△ABE(SAS).
(2)∵BC=2,BE=1,
∴CD=AD=AB=2,CE=3,
∴DE=![]() =
=![]() ,AE=
,AE=![]() =
=![]() ,
,
如圖,作AH⊥DE于H,
則S△AED=![]() DEAH,
DEAH,
又∵S△AED=![]() ADAB=2,
ADAB=2,
∴![]() DEAH=2,
DEAH=2,
∴AH=![]() ,
,
∴sin∠AED=![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形ABCD是矩形,AD∥x軸,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.

(1)直接寫出B、C、D三點的坐標;
(2)將矩形ABCD向右平移m個單位,使點A、C恰好同時落在反比例函數![]() (
(![]() )的圖象上,得矩形A′B′C′D′.求矩形ABCD的平移距離m和反比例函數的解析式.
)的圖象上,得矩形A′B′C′D′.求矩形ABCD的平移距離m和反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
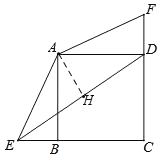
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經過A(-1,0),B(4,0),C(0,2)三點.
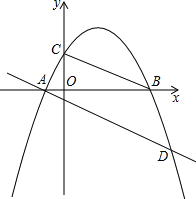
(1)求這條拋物線的解析式;
(2)E為拋物線上一動點,是否存在點E,使以A、B、E為頂點的三角形與△COB相似?若存在,試求出點E的坐標;若不存在,請說明理由;
(3)若將直線BC平移,使其經過點A,且與拋物線相交于點D,連接BD,試求出∠BDA的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC,BD相交于點O.E,F是AC上的兩點,并且AE=CF,連接DE,BF.
(1)求證:△DOE≌△BOF;
(2)若BD=EF,連接DE,BF.判斷四邊形EBFD的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x軸上,將Rt△AOB繞點O順時針旋轉至△RtA'OB',其中點B'落在反比例函數y=﹣![]() 的圖象上,OA'交反比例函數y=
的圖象上,OA'交反比例函數y=![]() 的圖象于點C,且OC=2CA',則k的值為( )
的圖象于點C,且OC=2CA',則k的值為( )

A. 4 B. ![]() C. 8 D. 7
C. 8 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王老師從學校出發,到距學校![]() 的某商場去給學生買獎品,他先步行了
的某商場去給學生買獎品,他先步行了![]() 后,換騎上了共享單車,到達商場時,全程總共剛好花了
后,換騎上了共享單車,到達商場時,全程總共剛好花了![]() .已知王老師騎共享單車的平均速度是步行速度的3倍(轉換出行方式時,所需時間忽略不計).
.已知王老師騎共享單車的平均速度是步行速度的3倍(轉換出行方式時,所需時間忽略不計).
(1)求王老師步行和騎共享單車的平均速度分別為多少?
(2)買完獎品后,王老師原路返回,為按時上班,路上所花時間最多只剩10分鐘,若王老師仍采取先步行,后換騎共享單車的方式返回,問:他最多可步行多少米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com