
【題目】如圖,在△ABC中,∠C=90°,AC=BC,斜邊AB=2,O是AB的中點,以O為圓心,線段OC的長為半徑畫圓心角為90°的扇形OEF,弧EF經過點C,則圖中陰影部分的面積為 . 
【答案】![]() ﹣
﹣ ![]()
【解析】解:連接OC,作OM⊥BC,ON⊥AC. 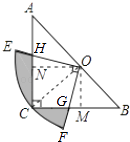
∵CA=CB,∠ACB=90°,點O為AB的中點,
∴OC= ![]() AB=1,四邊形OMCN是正方形,OM=
AB=1,四邊形OMCN是正方形,OM= ![]() .
.
則扇形FOE的面積是: ![]() =
= ![]() .
.
∵OA=OB,∠AOB=90°,點D為AB的中點,
∴OC平分∠BCA,
又∵OM⊥BC,ON⊥AC,
∴OM=ON,
∵∠GOH=∠MON=90°,
∴∠GOM=∠HON,
則在△OMG和△ONH中,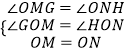 ,
,
∴△OMG≌△ONH(AAS),
∴S四邊形OGCH=S四邊形OMCN=( ![]() )2=
)2= ![]() .
.
則陰影部分的面積是: ![]() ﹣
﹣ ![]() .
.
故答案為: ![]() ﹣
﹣ ![]() .
.
連接OC,作OM⊥BC,ON⊥AC,證明△OMG≌△ONH,則S四邊形OGCH=S四邊形OMCN , 求得扇形FOE的面積,則陰影部分的面積即可求得.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:
【題目】如圖1,點A,B,O,C為數軸上四點,點A對應數a(a<﹣2),點O對應0,點C對應3,AB=2 (AB表示點A到點B的距離).
(1)填空:點C到原點O的距離 ,:點B對應的數 .(用含有a的式子)
(2)如圖2,將一刻度尺放在數軸上,刻度尺上“6cm”和“8.7cm”分別對應數軸上的點O和點C,若BC=5,求a的值和點A在刻度尺上對應的刻度.
(3)如圖3,在(2)的條件下,點A以1單位長度/秒的逮度向右運動,同時點C向左運動,若運動3秒時,點A和點C到原點D的距離相等,求點C的運動速度.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列變形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 兩邊同除以
兩邊同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移項,得7x=0;
④由方程2﹣![]() 兩邊同乘以6,得12﹣x﹣5=3(x+3).
兩邊同乘以6,得12﹣x﹣5=3(x+3).
錯誤變形的個數是( )個.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D為AB的中點,DE∥BC,交AC于點E,DE∥AC,交BC于點F.
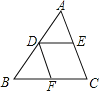
(1)求證:DE=BF;
(2)連接EF,請你猜想線段EF和AB有何關系?并對你的猜想加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,某市水費實行分段計費制,每戶每月用水量在規定用量及以下的部分收費標準相同,超出規定用量的部分收費標準相同.例如:若規定用量為10噸,每月用水量不超過10噸按1.5元/噸收費,超出10噸的部分按2元/噸收費,則某戶居民一個月用水8噸,則應繳水費:8×1.5=12(元);某戶居民一個月用水13噸,則應繳水費:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和繳納水費情況,根據表格提供的數據,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(噸) | 6 | 7 | 12 | 15 |
水費(元) | 12 | 14 | 28 | 37 |
(1)該市規定用水量為 噸,規定用量內的收費標準是 元/噸,超過部分的收費標準是 元/噸.
(2)若小明家五月份用水20噸,則應繳水費 元.
(3)若小明家六月份應繳水費46元,則六月份他們家的用水量是多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在2015年的政府工作報告中提出了九大熱詞,某數學興趣小組就A互聯網+、B民生底線、C中國制造2.0、D能耗強度等四個熱詞進行了抽樣調查,每個同學只能從中選擇一個“我最關注”的熱詞,如圖是根據調查結果繪制的兩幅不完整的統計圖. 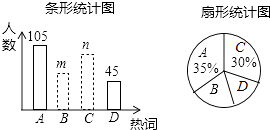
請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了名同學;
(2)條形統計圖中,m= , n=;
(3)扇形統計圖中,熱詞B所在扇形的圓心角的度數是;
(4)從該校學生中隨機抽取一個最關注熱詞D的學生的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩根木條,一根長20cm,另一根長24cm,將它們一端重合且放在同一條直線上,此時兩根木條的中點之間的距離為( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=13,DE是△ABC的中位線,F是DE的中點,已知B(-1,0),C(9,0),則點F的坐標為______________.
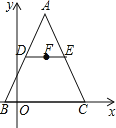
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖在長方形ABCD中,AB=12cm,BC=8cm,點P從A點出發,沿A→B→C→D路線運動,到D點停止;點Q從D點出發,沿D→C→B→A運動,到A點停止.若點P、點Q同時出發,點P的速度為每秒1cm,點Q的速度為每秒2cm,用x(秒)表示運動時間.
(1)求點P和點Q相遇時的x值.
(2)連接PQ,當PQ平分矩形ABCD的面積時,求運動時間x值.
(3)若點P、點Q運動到6秒時同時改變速度,點P的速度變為每秒3cm,點Q的速度為每秒1cm,求在整個運動過程中,點P、點Q在運動路線上相距路程為20cm時運動時間x值.
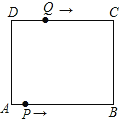


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com