
【題目】下面的圖像反映的過程是:小明從家去超市買文具,又去書店購書,然后回家.其中x表示時間,y表示小明離他家的距離,若小明家、超市、書店在同一條直線上.
根據圖像回答下列問題:

(1)超市離小明家多遠,小明走到超市用了多少時間?
(2)超市離書店多遠,小明在書店購書用了多少時間?
(3)書店離小明家多遠,小明從書店走回家的平均速度是每分鐘多少米?
科目:初中數學 來源: 題型:
【題目】聲音在空氣中傳播的速度y(米/秒)是氣溫x (攝氏度)的一次函數,下表列出了一組不同氣溫時的音速.
氣溫x/攝氏度 | 0 | 5 | 10 | 15 | 20 |
音速y/(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求y 與 x之間的函數關系式
(2)氣溫x=22(攝氏度)時,某人看到煙花燃放5秒后才聽到聲響,那么此人與燃放的煙花所在地相距多遠?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某升降機第一次上升5米,第二次又上升6米,第三次下降4米,第四次又下降7米。(上升記為正,下降記為負,單位:米)
(1)這時升降機與初始位置相距多少米?
(2)升降機共運行了多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y1=x+m的圖象與反比例函數![]() 的圖象交于A、B兩點.已知當x>1時,y1>y2;當0<x<1時,y1<y2.
的圖象交于A、B兩點.已知當x>1時,y1>y2;當0<x<1時,y1<y2.

(1)求一次函數的解析式;
(2)已知雙曲線在第一象限上有一點C到y軸的距離為3,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
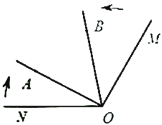
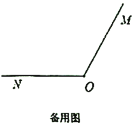
【題目】如圖,已知![]() ,射線
,射線![]() 從
從![]() 的位置開始繞點
的位置開始繞點![]() 按順時針方向旋轉,速度是每秒
按順時針方向旋轉,速度是每秒![]() ,同時射線
,同時射線![]() 從
從![]() 的位置開始繞點
的位置開始繞點![]() 按逆時針方向旋轉,速度是每秒
按逆時針方向旋轉,速度是每秒![]() ,設旋轉時間為
,設旋轉時間為![]() 秒
秒![]() .
.
(1)用含![]() 的代數式表示
的代數式表示![]() 和
和![]() 的度數;
的度數;
(2)在旋轉過程中,當![]() 等于
等于![]() 時,求
時,求![]() 的值;
的值;
(3)在旋轉過程中是否存在這樣的![]() ,使得射線
,使得射線![]() 恰好是圖中某個角的平分線?如果存在,請求出
恰好是圖中某個角的平分線?如果存在,請求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶市的重大惠民工程--公租房建設已陸續竣工,計劃10年內解決低收入人群的住房問題,前6年,每年竣工投入使用的公租房面積![]() 單位:百萬平方米
單位:百萬平方米![]() ,與時間x的關系是
,與時間x的關系是![]() 單位:年,
單位:年, ![]() 且x為整數
且x為整數![]() ;后4年,每年竣工投入使用的公租房面積
;后4年,每年竣工投入使用的公租房面積![]() 單位:百萬平方米
單位:百萬平方米![]() ,與時間x的關系是
,與時間x的關系是![]() 單位:年,
單位:年, ![]() 且x為整數
且x為整數![]() 假設每年的公租房全部出租完
假設每年的公租房全部出租完![]() 另外,隨著物價上漲等因素的影響,每年的租金也隨之上調,預計,第x年投入使用的公租房的租金
另外,隨著物價上漲等因素的影響,每年的租金也隨之上調,預計,第x年投入使用的公租房的租金![]() 單位:元
單位:元![]() 與時間
與時間![]() 單位:年,
單位:年, ![]() 且x為整數
且x為整數![]() 滿足一次函數關系如下表:
滿足一次函數關系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z與x的函數關系式;
求出z與x的函數關系式;
![]() 求政府在第幾年投入的公租房收取的租金最多,最多為多少百萬元;
求政府在第幾年投入的公租房收取的租金最多,最多為多少百萬元;
![]() 若第6年竣工投入使用的公租房可解決20萬人的住房問題,政府計劃在第10年投入的公租房總面積不變的情況下,要讓人均住房面積比第6年人均住房面積提高
若第6年竣工投入使用的公租房可解決20萬人的住房問題,政府計劃在第10年投入的公租房總面積不變的情況下,要讓人均住房面積比第6年人均住房面積提高![]() ,這樣可解決住房的人數將比第6年減少
,這樣可解決住房的人數將比第6年減少![]() ,求a的值.
,求a的值.
![]() 參考數據:
參考數據: ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,已知直線AB的函數解析式為y=﹣2x+8,與x軸交于點A,與y軸交于點B.
(1)求A、B兩點的坐標;
(2)若點P(m,n)為線段AB上的一個動點(與A、B不重合),作PE⊥x軸于點E,PF⊥y軸于點F,連接EF,問:
①若△PAO的面積為S,求S關于m的函數關系式,并寫出m的取值范圍;
②是否存在點P,使EF的值最小?若存在,求出EF的最小值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了全面提高學生的能力,學校組織課外活動小組,并要求初一學年積極參加,初一學年共有四個班,參加的學生共有(6a﹣3b)人,其中一班有a人參加,二班參加的人數比一班參加的人數兩倍少b人,三班參加的人數比二班參加的人數一半多1人.
(1)求三班的人數(用含a,b的式子表示);
(2)求四班的人數(用含a,b的式子表示);
(3)若四個班共54人參加了課外活動,求二班比三班多多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售甲、乙兩種商品,現有如下信息:
請結合以上信息,解答下列問題:
(1)求甲、乙兩種商品的進貨單價;
(2)已知甲、乙兩種商品的零售單價分別為2元、3元,該商店平均每天賣出甲商品500件和乙商品1300件,經市場調查發現,甲種商品零售單價每降0.1元,甲種商品每天可多銷售100件,商店決定把甲種商品的零售單價下降m(m>0)元,在不考慮其他因素的條件下,求當m為何值時,商店每天銷售甲、乙兩種商品獲取的總利潤為1800元(注:單件利潤=零售單價﹣進貨單價)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com