
【題目】(1)如圖①,Rt△ABC中,∠C=90°,AC=3,BC=4.點D是AB邊上任意一點,則CD的最小值為 。
(2)如圖②,在矩形ABCD中,AB=3,BC=4.點M、N分別在BD、BC上。求CM+MN的最小值.
(3)如圖③,在矩形ABCD中,AB=3,BC=4.點E是AB邊上的一點,且AE=2,點F是BC邊上的任意一點。把△BEF沿EF翻折,點B對應點G,連接AG、CG.四邊形AGCD的面積的最小值是 。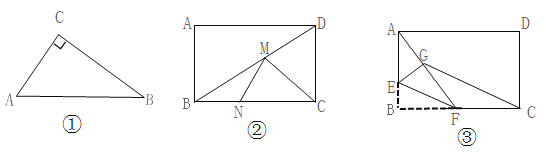
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)根據點到直線的距離最小,再用三角形的面積即可得出結論;
(2)先根據軸對稱確定出點M和N的位置,再利用面積求出CF,進而求出CE,最后用三角函數即可求出CM+MN的最小值;
(3)先確定出EG⊥AC時,四邊形AGCD的面積最小,再用銳角三角函數求出點G到AC的距離,最后用面積之和即可得出結論.
(1)如圖①,
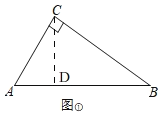
過點C作CD⊥AB于D,根據點到直線的距離垂線段最小,此時CD最小,
在Rt△ABC中,AC=3,BC=4,根據勾股定理得,AB=5,
∵![]() AC×BC=
AC×BC=![]() AB×CD,
AB×CD,
∴CD=![]() =
=![]() ,
,
故答案為:![]() ;
;
2)如圖②,
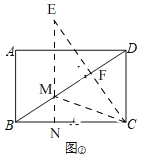
作出點C關于BD的對稱點E,
過點E作EN⊥BC于N,交BD于M,連接CM,此時CM+MN=EN最小;
∵四邊形ABCD是矩形,
∴∠BCD=90°,CD=AB=3,根據勾股定理得,BD=5,
∵CE⊥BC,
∴![]() BD×CF=
BD×CF=![]() BC×CD,
BC×CD,
∴CF=![]() =
=![]() ,
,
由對稱得,CE=2CF=![]() ,
,
在Rt△BCF中,cos∠BCF=![]() =
=![]() ,
,
∴sin∠BCN=![]() ,
,
在Rt△CEN中,EN=CEsin∠BCE=![]() =
=![]() ;
;
即:CM+MN的最小值為![]() ;
;
(3)如圖,
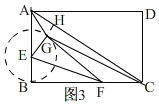
∵四邊形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根據勾股定理得,AC=5,
∵AB=3,AE=2,
∴點F在BC上的任何位置時,點G始終在AC的下方,
設點G到AC的距離為h,
∵S四邊形AGCD=S△ACD+S△ACG=![]() AD×CD+
AD×CD+![]() AC×h=
AC×h=![]() ×4×3+
×4×3+![]() ×5×h=
×5×h=![]() h+6,
h+6,
∴要四邊形AGCD的面積最小,即:h最小,
∵點G是以點E為圓心,BE=1為半徑的圓上在矩形ABCD內部的一部分點,
∴EG⊥AC時,h最小,
由折疊知∠EGF=∠ABC=90°,
延長EG交AC于H,則EH⊥AC,
在Rt△ABC中,sin∠BAC=![]() ,
,
在Rt△AEH中,AE=2,sin∠BAC=![]() ,
,
∴EH=![]() ,AE=
,AE=![]() ,
,
∴h=EH-EG=![]() -1=
-1=![]() ,
,
∴S四邊形AGCD最小=![]() h+6=
h+6=![]() ×
×![]() +6=
+6=![]() .
.


科目:初中數學 來源: 題型:
【題目】在平整的地面上,由若干個完全相同的棱長為 10 cm 的小正方體堆成一個幾何體,如圖 所示.
(1)這個幾何體由多少個小正方體組成?請畫出這個幾何體的三視圖.
(2)如果在這個幾何體的表面(不包括底面)噴上黃色的漆,則在所有的小正方體中,有多少個只有一個面是黃色?有多少個只有兩個面是黃色?有多少個只有三個面是黃色?
(3)假設現在你手里還有一些相同的小正方體,保持這個幾何體的主視圖、俯視圖形狀 不變,最多可以再添加幾個小正方體?這時如果要重新給這個幾何體表面(不包括底面) 噴上紅色的漆,需要噴漆的面積比原幾何體增加了還是減少了?增加或減少的面積是 多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD,AB=AC,E、F分別是BC、AD的中點,連接AE、CF.
(1)求證:四邊形AECF是矩形;
(2)若AB=6,求菱形的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用正方形硬紙板做三棱柱盒子,每個盒子由3個矩形側面和2個正三角形底面組成。硬紙板以如圖兩種方式裁剪(裁剪后邊角料不再利用)
A方法:剪6個側面; B方法:剪4個側面和5個底面。

現有19張硬紙板,裁剪時![]() 張用A方法,其余用B方法。
張用A方法,其余用B方法。
(1)用![]() 的代數式分別表示裁剪出的側面和底面的個數;
的代數式分別表示裁剪出的側面和底面的個數;
(2)若裁剪出的側面和底面恰好全部用完,問能做多少個盒子?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著手機的普及,微信![]() 一種聊天軟件
一種聊天軟件![]() 的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況
的興起,許多人抓住這種機會,做起了“微商”,很多農產品也改變了原來的銷售模式,實行了網上銷售,這不剛大學畢業的小明把自家的冬棗產品也放到了網上,他原計劃每天賣100斤冬棗,但由于種種原因,實際每天的銷售量與計劃量相比有出入,下表是某周的銷售情況![]() 超額記為正,不足記為負
超額記為正,不足記為負![]() 單位:斤
單位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
與計劃量的差值 |
|
|
|
|
|
|
|
(1)根據記錄的數據可知前三天共賣出 ______ 斤;
(2)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售 ______ 斤;
(3)本周實際銷售總量達到了計劃數量沒有?
(4)若冬季每斤按8元出售,每斤冬棗的運費平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,點P、Q分別是CD、AD的中點,動點E從點A向點B運動,到點B時停止運動;同時,動點F從點P出發,沿P→D→Q運動,點E、F的運動速度相同.設點E的運動路程為x,△AEF的面積為y,能大致刻畫y與x的函數關系的圖象是( )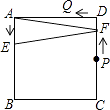
A.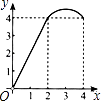
B.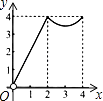
C.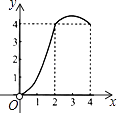
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十·一”黃金周期間,武漢動物園在7天假期中每天旅游的人數變化如下表(正數表示比前一天多的人數,負數表示比前一天少的人數)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人數變化單位:萬人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人數記為![]() ,請用
,請用![]() 的代數式表示10月2日的游客人數?
的代數式表示10月2日的游客人數?
(2)請判斷七天內游客人數最多的是哪天?請說明理由。
(3)若9月30日的游客人數為2萬人,門票每人10元。問黃金周期間武漢動物園門票收入是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx﹣3的對稱軸為直線x=1,交x軸于A、B兩點,交y軸于C點,其中B點的坐標為(3,0). 
(1)直接寫出A點的坐標;
(2)求二次函數y=ax2+bx﹣3的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com