
【題目】如圖,△ABC中,⊙O經過A、B兩點,且交AC于點D,連接BD,∠DBC=∠BAC.
(1)證明BC與⊙O相切;
(2)若⊙O的半徑為6,∠BAC=30°,求圖中陰影部分的面積.
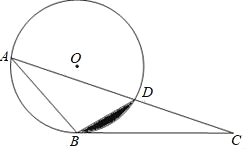
【答案】(1)證明見解析;(2)6π-9![]() .
.
【解析】
(1)連接BO并延長交⊙O于點E,連接DE.由圓周角定理得出∠BDE=90°,再求出∠EBD+∠DBC=90°,根據切線的判定定理即可得出BC是⊙O的切線;
(2)分別求出等邊三角形DOB的面積和扇形DOB的面積,即可求出答案.
(1)證明:連接BO并延長交⊙O于點E,連接DE,
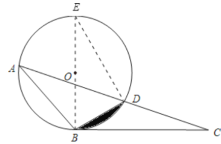
∵BE是直徑,∴∠EDB=90°,
∴∠E+∠EBD=90°
∵![]() =
=![]() ,∴∠E=∠A
,∴∠E=∠A
又∵∠DBC=∠BAC,∴∠DBC=∠E
∴∠DBC+∠EBD=90°,∴∠EBC=90°,∴BC⊥EB.
又∵OB是半徑(B在⊙O上),∴BC與⊙O相切.
(2)∵![]() =
=![]() ,∴∠BOD=2∠A=60°
,∴∠BOD=2∠A=60°
S陰影= S扇形OBD-S△OBD=π36×![]() -9
-9![]() =6π-9
=6π-9![]() .
.


科目:初中數學 來源: 題型:
【題目】若一個四位自然數n滿足千位與個位相同,百位與十位相同,我們稱這個數為“天平數”.將“天平數”n的前兩位與后兩位交換位置得到一個新的“天平數”n′,記F(n)=![]() ,例如n=2112,n′=1221,F(2112)=
,例如n=2112,n′=1221,F(2112)=![]() =9
=9
(1)計算F(5335)= ;若“天平數”n滿足F(n)是一個完全平方數,求F(n)的值;
(2)s、t“天平數“,其中s=![]() ,t=
,t=![]() (1≤b<a≤9,1≤x<y≤9且a,b, xy為整數),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,規定:K(s,t)=
(1≤b<a≤9,1≤x<y≤9且a,b, xy為整數),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,規定:K(s,t)=![]() ,求K(s,t)的所有結果的值.
,求K(s,t)的所有結果的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】曉琳和爸爸到太子河公園運動,兩人同時從家出發,沿相同路線前行,途中爸爸有事返回,曉琳繼續前行5分鐘后也原路返回,兩人恰好同時到家.曉琳和爸爸在整個運動過程中離家的路程y1(米),y2(米)與運動時間x(分)之間的函數關系如圖所示,下列結論:①兩人同行過程中的速度為200米/分;②m的值是15,n的值是3000;③曉琳開始返回時與爸爸相距1800米;④運動18分鐘或30分鐘時,兩人相距900米.其中正確結論的個數是( )
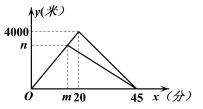
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
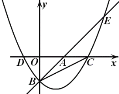
【題目】如圖,直線y=x-3與坐標軸交于A、B兩點,拋物線![]() 經過點B,與直線y=x-3交于點E(8,5),且與x軸交于C,D兩點.
經過點B,與直線y=x-3交于點E(8,5),且與x軸交于C,D兩點.
(1)求拋物線的解析式;
(2)拋物線上有一點M,當∠MBE=75°時,求點M的橫坐標;
(3)點P在拋物線上,在坐標平面內是否存在點Q,使得以點P,Q,B,C為頂點的四邊形是矩形?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮從家出發步行到公交站臺后,等公交車去學校,如圖, 折線表示這個過程中行程 s (千米)與所花時間 t (分)之間的關系,下 列說法錯誤的是( )
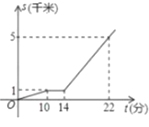
A.他家到公交車站臺需行 1 千米B.他等公交車的時間為 4 分鐘
C.公交車的速度是 500 米/分D.他步行與乘公交車行駛的平均速度300米/分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
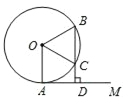
【題目】如圖,AM為⊙O的切線,A為切點,過⊙O上一點B作BD⊥AM于點D,BD交⊙O于C,OC平分∠AOB.
(1)求∠AOB的度數;
(2)若線段CD的長為2cm,求![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,兩個完全相同的三角形紙片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
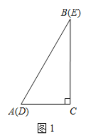

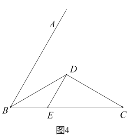
(1)操作發現:如圖2,固定![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當點
旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,填空:①線段
邊上時,填空:①線段![]() 與
與![]() 的位置關系是________;②設
的位置關系是________;②設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的數量關系是_____.
的數量關系是_____.
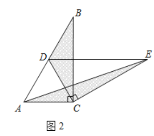
(2)猜想論證:當![]() 繞點
繞點![]() 旋轉到如圖3所示的位置時,請猜想(1)中
旋轉到如圖3所示的位置時,請猜想(1)中![]() 與
與![]() 的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() (如圖4).若在射線
(如圖4).若在射線![]() 上存在點
上存在點![]() ,使
,使![]() ,請求相應的
,請求相應的![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
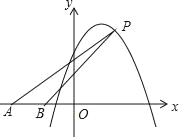
【題目】如圖,在平面直角坐標系中,點A、B的坐標分別為(﹣5,0)、(﹣2,0).點P在拋物線y=﹣2x2+4x+8上,設點P的橫坐標為m.當0≤m≤3時,△PAB的面積S的取值范圍是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
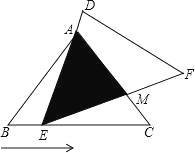
【題目】如圖,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,將△DEF與△ABC重合在一起,△ABC不動,△DEF運動,并滿足:點E在邊BC上沿B到C的方向運動,且DE始終經過點A,EF與AC交于M點.
(1)求證:△ABE∽△ECM;
(2)探究:在△DEF運動過程中,重疊部分能否構成等腰三角形?若能,求出BE的長;若不能,請說明理由;
(3)當線段BE為何值時,線段AM最短,最短是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com