
【題目】已知x2=1,求![]() 的值.
的值.
解:因為![]() ,所以
,所以![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]() 無意義
無意義
所以![]() 的值是1
的值是1
(1)錯因:_________________________________.
(2)糾錯: _________________________________.
科目:初中數學 來源: 題型:
【題目】為了提高學生書寫漢字的能力,增強保護漢子的意識,某校舉辦了首屆“漢字聽寫大賽”,學生經選拔后進入決賽,測試同時聽寫100個漢字,每正確聽寫出一個漢字得1分,本次決賽,學生成績為![]() (分),且
(分),且![]() ,將其按分數段分為五組,繪制出以下不完整表格:
,將其按分數段分為五組,繪制出以下不完整表格:
組別 | 成績 | 頻數(人數) | 頻率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
請根據表格提供的信息,解答以下問題:
(1)本次決賽共有 名學生參加;
(2)直接寫出表中a= ,b= ;
(3)請補全下面相應的頻數分布直方圖;

(4)若決賽成績不低于80分為優秀,則本次大賽的優秀率為 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔賽跑”是同學們熟悉的寓言故事.如圖所示,表示了寓言中的龜、兔的路程S和時間t的關系(其中直線段表示烏龜,折線段表示兔子).下列敘述正確的是( )
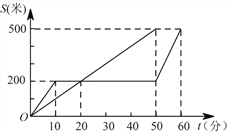
A. 賽跑中,兔子共休息了50分鐘
B. 烏龜在這次比賽中的平均速度是0.1米/分鐘
C. 兔子比烏龜早到達終點10分鐘
D. 烏龜追上兔子用了20分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(11分)如圖,拋物線y=ax2+bx﹣3與x軸交于A,B兩點,與y軸交于C點,且經過點(2,﹣3a),對稱軸是直線x=1,頂點是M.
(1)求拋物線對應的函數表達式;
(2)經過C,M兩點作直線與x軸交于點N,在拋物線上是否存在這樣的點P,使以點P,A,C,N為頂點的四邊形為平行四邊形?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)設直線y=﹣x+3與y軸的交點是D,在線段BD上任取一點E(不與B,D重合),經過A,B,E三點的圓交直線BC于點F,試判斷△AEF的形狀,并說明理由;
(4)當E是直線y=﹣x+3上任意一點時,(3)中的結論是否成立(請直接寫出結論).
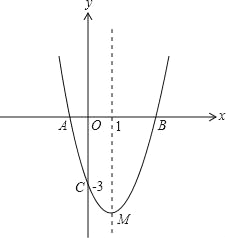
查看答案和解析>>
科目:初中數學 來源: 題型:
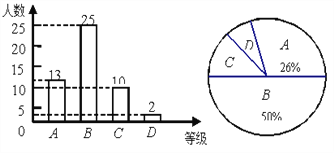
【題目】某一中學以1班學生的地理測試成績為樣本,按A、B、C、D四個等級進行統計,并將統計結果繪制成兩幅統計圖,結合圖中信息解答下列問題:
(1)D級學生的人數占全班人數的百分比為________;
(2)扇形統計圖中C級所在扇形圓心角度數為__________;
(3)若該校共有1500人,則估計該校地理成績得A級的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你發現了什么規律?請用語言敘述這個規律:______________________________.
(3)根據你發現的規律填空:
①已知![]() =1.442,則
=1.442,則![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,則
=0.076 96,則![]() =__________.
=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
(1)如果點P到點A,點B的距離相等,那么x=______;
(2)當x=______時,點P到點A,點B的距離之和是6;
(3)若點P到點A,點B的距離之和最小,則x的取值范圍是______;
(4)在數軸上,點M,N表示的數分別為x![]() ,x
,x![]() ,我們把x
,我們把x![]() ,x
,x![]() 之差的絕對值叫做點M,N之間的距離,即MN="|" x
之差的絕對值叫做點M,N之間的距離,即MN="|" x![]() -x
-x![]() |.若點P以每秒3個單位長度的速度從點O沿著數軸的負方向運動時,點E以每秒1個單位長度的速度從點A沿著數軸的負方向運動、點F以每秒4個單位長度的速度從點B沿著數軸的負方向運動,且三個點同時出發,那么運動______秒時,點P到點E,點F的距離相等.
|.若點P以每秒3個單位長度的速度從點O沿著數軸的負方向運動時,點E以每秒1個單位長度的速度從點A沿著數軸的負方向運動、點F以每秒4個單位長度的速度從點B沿著數軸的負方向運動,且三個點同時出發,那么運動______秒時,點P到點E,點F的距離相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在實施城鄉清潔工作過程中,某校對各個班級教室衛生情況的考評包括以下幾項:黑板、門窗、桌椅、地面.一天,兩個班級的各項衛生成績分別如下表:(單位:分)
| 黑板 | 門窗 | 桌椅 | 地面 |
一班 | 95 | 85 | 89 | 91 |
二班 | 90 | 95 | 85 | 90 |
(1)兩個班的平均得分分別是多少?
(2)按學校的考評要求,將黑板、門窗、桌椅、地面這四項得分依次按15%、10%、35%、40%的權重計算各班的衛生成績,那么哪個班的衛生成績較高?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了順利通過“國家文明城市”驗收,市政府擬對部分路段的人行道地磚、綠化帶、排水管等公用設施全面更新改造,根據市政建設的需要,需在40天內完成工程.現有甲、乙兩個工程隊有意承包這項工程,經調查知道,乙工程隊單獨完成此項工程的時間是甲工程隊單獨完成此項工程時間的2倍,若甲、乙兩工程隊合作只需10天完成.
(1)甲、乙兩個工程隊單獨完成此項工程各需多少天?
(2)若甲工程隊每天的費用是4.5萬元,乙工程隊每天的工程費用是2.5萬元,請你設計一種方案,既能按時完成工程,又能使工程費用最少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com