
【題目】甲、乙兩車從A城出發沿相同的路線勻速行駛至B城.在整個行駛過程中,甲、乙兩車離開A城的距離y(千米)與甲車行駛的時間t(小時)之間的函數關系如圖所示,則下列結論:①A、B兩城相距300千米;②乙車比甲車晚出發1小時,卻早到1小時;③乙車出發后2.5小時追上甲車;④當甲、乙兩車相距50千米時,t=![]() 或
或![]() .其中正確的是________(填序號).
.其中正確的是________(填序號).

【答案】①②
【解析】由圖象可知A、B兩城市之間的距離為300km,甲行駛的時間為5小時,而乙是在甲出發1小時后出發的,且用時3小時,即比甲早到1小時,
∴①②都正確;
設甲車離開A城的距離y與t的關系式為y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
設乙車離開A城的距離y與t的關系式為y乙=mt+n,
把(1,0)和(4,300)代入可得![]() ,解得
,解得![]() ,
,
∴y乙=100t-100,
令y甲=y乙可得:60t=100t-100,解得t=2.5,
即甲、乙兩直線的交點橫坐標為t=2.5,
此時乙出發時間為1.5小時,即乙車出發1.5小時后追上甲車,
∴③不正確;
令|y甲-y乙|=50,可得|60t-100t+100|=50,即|100-40t|=50,
當100-40t=50時,可解得t=![]() ,
,
當100-40t=-50時,可解得t=![]() ,
,
又當t=![]() 時,y甲=50,此時乙還沒出發,
時,y甲=50,此時乙還沒出發,
當t=![]() 時,乙到達B城,y甲=250;
時,乙到達B城,y甲=250;
綜上可知當t的值為![]() 或
或![]() 或
或![]() 或t=
或t=![]() 時,兩車相距50千米,
時,兩車相距50千米,
∴④不正確;
故答案是:③,④。


科目:初中數學 來源: 題型:
【題目】如圖,某足球運動員站在點O處練習射門,將足球從離地面0.5m的A處正對球門踢出(點A在y軸上),足球的飛行高度y(單位:m)與飛行時間t(單位:s)之間滿足函數關系y=at2+5t+c,已知足球飛行0.8s時,離地面的高度為3.5m. 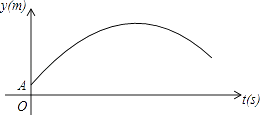
(1)足球飛行的時間是多少時,足球離地面最高?最大高度是多少?
(2)若足球飛行的水平距離x(單位:m)與飛行時間t(單位:s)之間具有函數關系x=10t,已知球門的高度為2.44m,如果該運動員正對球門射門時,離球門的水平距離為28m,他能否將球直接射入球門?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2﹣(2k﹣3)x+k2+1=0有兩個不相等的實數根x1、x2 .
(1)求k的取值范圍;
(2)試說明x1<0,x2<0;
(3)若拋物線y=x2﹣(2k﹣3)x+k2+1與x軸交于A、B兩點,點A、點B到原點的距離分別為OA、OB,且OA+OB=2OAOB﹣3,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為半圓直徑,D、E為圓周上兩點,且AD=DE,AE與BD交于點C,則圖中與∠BCE相等的角有( ) 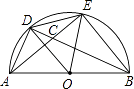
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列一元一次方程解應用題:
學生在素質教育基地進行社會實踐活動,幫助農民伯伯采摘了黃瓜和茄子共80千克,了解到這些蔬菜的種植成本共180元,還了解到如下信息:
(1)求采摘的黃瓜和茄子各多少千克?
(2)這些采摘的黃瓜和茄子可賺多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點![]() 是反比例函數
是反比例函數![]() 在第一象限圖像上的一個動點,連接
在第一象限圖像上的一個動點,連接![]() ,以
,以![]() 為長,
為長,![]() 為寬作矩形
為寬作矩形![]() ,且點
,且點![]() 在第四象限,隨著點
在第四象限,隨著點![]() 的運動,點
的運動,點![]() 也隨之運動,但點
也隨之運動,但點![]() 始終在反比例函數
始終在反比例函數![]() 的圖像上,則
的圖像上,則![]() 的值為( )
的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com