Question

【題目】如圖，在Rt△ACB中，∠C＝90°，D是AB上一點，以BD為直徑的⊙O與AC相切于點E，交BC于點F，連接DF.

(1)求證：DF＝2CE；

(2)若BC＝3，sinB＝，求線段BF的長．

Answer 1

【答案】（1）證明見解析；（2）線段BF的長為

【解析】試題分析：（1）連接OE交DF于G，首先證明四邊形EGFC是矩形，再根據垂徑定理即可證明．（2）設OE=x，由OE∥BC，得△AOE∽△ABC，得=，列出方程求出x，再在Rt△BDF中，由sinB=，推出cosB==，即可解決問題．

試題解析：(1)連接OE，交DF于點G，

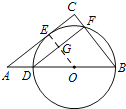
∵AC切⊙O于點E，

∴∠CEO＝90°.

又∵BD為⊙O的直徑，

∴∠DFC＝∠DFB＝90°.

∵∠C＝90°，

∴四邊形CEGF為矩形．

∴CE＝GF，∠EGF＝90°，

∴DF＝2CE　

(2)在Rt△ABC中，

∵∠C＝90°，BC＝3，sinB＝，

∴AB＝5，設OE＝x，

∵OE∥BC，

∴△AOE∽△ABC.

∴，

∴，

∴x＝，

∴BD＝.

在Rt△BDF中，∵∠DFB＝90°，sinB＝，

∴cosB＝＝，

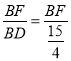∴BF＝