
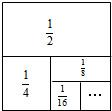
利用圖形來表示數量或數量關系,也可以利用數量或數量關系來描述圖形特征或圖形之間的關系,這種思想方法稱為數形結合.我們剛學過的第9章《整式乘法與因式分解》就很好地體現了這一思想方法,你能利用數形結合的思想解決下列問題嗎?
(1)如圖,一個邊長為1的正方形,依次取正方形面積的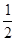 、
、 、
、
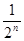 ,根據圖示我們可以知道:
,根據圖示我們可以知道: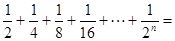 .
.

利用上述公式計算: .
.
(2)計算: ;
;
(3)計算: .
.
 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 2n |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |

| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 81 |
| 2n-1 |
| 3n |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
 n次取走后,還剩
n次取走后,還剩| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 2n-1 |
| 3n |
| 2n |
| 3n |
| 2n |
| 3n |
查看答案和解析>>
科目:初中數學 來源:2013年初中數學單元提優測試卷-平方差公式(解析版) 題型:解答題
利用圖形來表示數量或數量關系,也可以利用數量或數量關系來描述圖形特征或圖形之間的關系,這種思想方法稱為數形結合.我們剛學過的《從面積到乘法公式》就很好地體現了這一思想方法,你能利用數形結合的思想解決下列問題嗎?
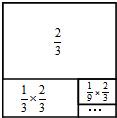
如圖,一個邊長為1的正方形,依次取正方形的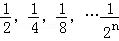 ,根據圖示我們可以知道:第一次取走
,根據圖示我們可以知道:第一次取走 后還剩
后還剩 ,即
,即 =1﹣
=1﹣ ;前兩次取走
;前兩次取走 +
+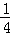 后還剩
后還剩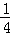 ,即
,即 +
+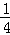 =1﹣
=1﹣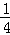 ;前三次取走
;前三次取走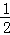 +
+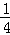 +
+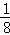 后還剩
后還剩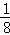 ,即
,即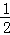 +
+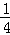 +
+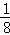 =1﹣
=1﹣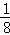 ;…前n次取走后,還剩 _________ ,即 _________ = _________ .
;…前n次取走后,還剩 _________ ,即 _________ = _________ .
利用上述計算:
(1)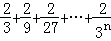 = _________ .
= _________ .
(2)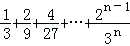 = _________ .
= _________ .
(3)2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012(本題寫出解題過程)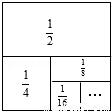
查看答案和解析>>
科目:初中數學 來源:2014屆江蘇省劉潭實驗學校七年級下學期期中考試數學卷(解析版) 題型:解答題
利用圖形來表示數量或數量關系,也可以利用數量或數量關系來描述圖形特征或圖形之間的關系,這種思想方法稱為數形結合.我們剛學過的《從面積到乘法公式》就很好地體現了這一思想方法,你能利用數形結合的思想解決下列問題嗎?
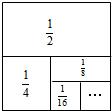
如圖,一個邊長為1的正方形,依次取正方形的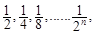 根據圖示我們可以知道:第一次取走
根據圖示我們可以知道:第一次取走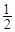 后還剩
后還剩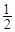 ,即
,即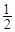 =1-
=1-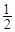 ;前兩次取走
;前兩次取走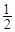 +
+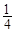 后還剩
后還剩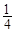 ,即
,即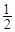 +
+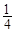 =1-
=1-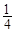 ;前三次取走
;前三次取走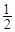 +
+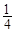 +
+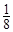 后還剩
后還剩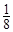 ,即
,即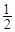 +
+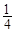 +
+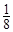 =1-
=1-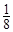 ;……前n次取走后,還剩
,
;……前n次取走后,還剩
,
即 = .
利用上述計算:
(1) 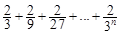 =
.
=
.
(2) 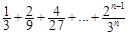 =
.
=
.
(3) 2-22-23-24-25-26-…-22011+22012 (本題寫出解題過程)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com