
【題目】已知,如圖,在△ABC中,AB=8cm,AC=4cm,△BAC的平分線AD與BC的垂直平分線DG交于點D,過點D的直線DE⊥AB于點E,DF⊥AC于點F.
(1)求證:BE=CF;
(2)求AE的長.

【答案】(1)見解析;(2)AE=6cm.
【解析】
(1)利用角平分線的性質得出DE=DF,連接BD,CD.利用垂直平分線的性質得出DB=DC,證得Rt△DCF≌Rt△DBE,得出結論;
(2)易證Rt△AED≌Rt△AFD,可得AE=AF,結合(1)的結論,利用線段的和與差得出答案即可.
(1)證明:∵點D在∠BAC的平分線上,DE⊥AB,DF⊥AC,
∴DE=DF.
連接BD,CD.
∵點D在BC的垂直平分線上,
∴DB=DC;
在Rt△DCF與Rt△DBE中,![]() ,
,
∴Rt△DCF≌Rt△DBE(HL),
∴BE=CF;
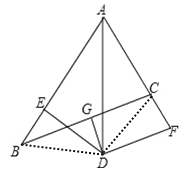
(2)解:∵DE=DF.
在Rt△AED與Rt△AFD中,![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AB=8cm,AC=4cm,BE=CF,AE=AF=AC+CF,
∴AB=AE+BE=AC+BE+CF=AC+2BE,
∴BE=2cm,
∴AE=ABBE=6cm.


科目:初中數學 來源: 題型:
【題目】已知數軸上有A,B兩點,分別表示﹣40,20,甲、乙兩只螞蟻分別從A,B兩點同時出發,甲沿線段AB方向以3個單位長度/秒的速度向右運動,甲到達點B處時運動停止;乙沿線段BA方向以5個單位長度/秒的速度向左運動.
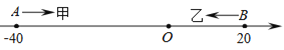
(1)求甲、乙第一次相遇點所表示的數.
(2)求經過多少秒時,甲、乙相距28個單位長度?
(3)若乙到達A點后立刻掉頭追趕甲(速度保持不變),則在甲到達B點前,甲、乙是否還能再次相遇?若能,求出相遇點所表示的數;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在數軸上有![]() 兩點,點
兩點,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 在
在![]() 點的左邊,且
點的左邊,且![]() .若有一動點
.若有一動點![]() 從數軸上點
從數軸上點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿數軸向左勻速運動,動點
個單位長度的速度沿數軸向左勻速運動,動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單 位長度的速度沿著數軸向右勻速運動,設運動時間為
個單 位長度的速度沿著數軸向右勻速運動,設運動時間為![]() 秒,解決以下問題:
秒,解決以下問題:
![]() 寫出數軸上點
寫出數軸上點![]() 所表示的數;
所表示的數;
![]() 若點
若點![]() 分別從
分別從![]() 兩點同時出發,問點
兩點同時出發,問點![]() 運動多少秒與點
運動多少秒與點![]() 相距
相距![]() 個單位長度?
個單位長度?
![]() 探索問題:若
探索問題:若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,當點
的中點,當點![]() 在線段
在線段![]() 上運動過程中,探索線段
上運動過程中,探索線段![]() 與線段
與線段![]() 的數量關系(寫出過程).
的數量關系(寫出過程).

查看答案和解析>>
科目:初中數學 來源: 題型:
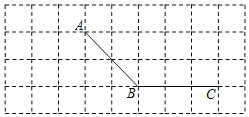
【題目】如圖,所有小正方形的邊長都為1個單位,A、B、C均在格點上.
![]() 過點C畫線段AB的平行線CD;
過點C畫線段AB的平行線CD;
![]() 過點A畫線段BC的垂線,垂足為E;
過點A畫線段BC的垂線,垂足為E;
![]() 過點A畫線段AB的垂線,交線段CB的延長線于點F;
過點A畫線段AB的垂線,交線段CB的延長線于點F;
![]() 線段AE的長度是點______到直線______的距離;
線段AE的長度是點______到直線______的距離;
![]() 線段AE、BF、AF的大小關系是______
線段AE、BF、AF的大小關系是______![]() 用“
用“![]() ”連接
”連接![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源.某城市環保部門為了提高宣傳實效,抽樣調查了部分居民小區一段時間內生活垃圾的分類情況,其相關信息如下:
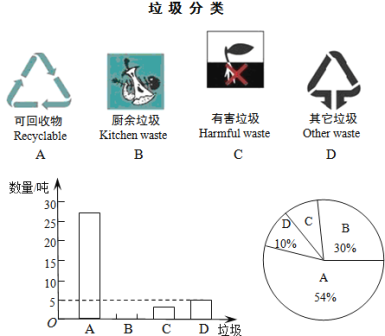
根據圖表解答下列問題:
(1)請將條形統計圖補充完整;
(2)在扇形統計圖樣中,產生的有害垃圾C所對應的圓心角 度;
(3)調查發現,在可回收物中塑料類垃圾占13%,每回收1噸塑料類垃圾可獲得0.5噸二級原料.假設該城市每月產生的生活垃圾為1000噸,且全部分類處理,那么每月回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面推理過程:
如圖,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代換).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代換).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是某校“河南省漢子聽寫大賽初賽”冠軍組成員的年齡分布
年齡/歲 | 12 | 13 | 14 | 15 |
人數 | 5 | 15 | x | 12﹣x |
對于不同的x,下列關于年齡的統計量不會發生改變的是( )
A. 平均數、中位數 B. 平均數、方差 C. 眾數、中位數 D. 中位數、方差
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是⊙O的直徑,弦CD⊥AB于H,過CD延長線上一點E作⊙O的切線交AB的延長線于F,切點為G,連接AG交CD于K.
(1)如圖1,求證:KE=GE;
(2)如圖2,連接CABG,若∠FGB=![]() ∠ACH,求證:CA∥FE;
∠ACH,求證:CA∥FE;
(3)如圖3,在(2)的條件下,連接CG交AB于點N,若sinE=![]() ,AK=
,AK=![]() ,求CN的長.
,求CN的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com