
【題目】如圖,![]() 為
為![]() 的直徑,弦
的直徑,弦![]() ,
,![]() 相交于點
相交于點![]() ,且
,且![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
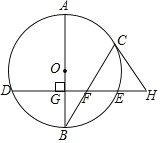
(1)求證:![]() ;
;
(2)若![]() 的半徑為5,點
的半徑為5,點![]() 是
是![]() 的中點,
的中點,![]() ,寫出求線段
,寫出求線段![]() 長的思路.
長的思路.
【答案】(1)見解析;(2)求解思路見解析.
【解析】
(1)連接OC,根據切線定理可知![]() ,根據
,根據![]() 得到
得到![]() ,利用同圓半徑相等得到
,利用同圓半徑相等得到![]() ,進而得到
,進而得到![]() ,再利用對頂角以及等量代換即可完成.
,再利用對頂角以及等量代換即可完成.
(2)思路一:①![]() 過圓心且點
過圓心且點![]() 是
是![]() 的中點,由垂徑定理可得
的中點,由垂徑定理可得![]() ,
,![]() ;
;
②由![]() 與
與![]() 互余,
互余,![]() 與
與![]() 互余可得
互余可得![]() ,從而可知
,從而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可設
,可設![]() ,
,![]() ,由勾股定
,由勾股定
理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的長.
的長.
思路二:連接![]() ,如圖3.
,如圖3.
①由![]() 是
是![]() 的直徑,可得
的直徑,可得![]() 是直角三角形,知
是直角三角形,知![]() 與
與![]() 互余,
互余,
又![]() 可知
可知![]() 與
與![]() 互余,得
互余,得![]() ;
;
②由![]() ,
,![]() ,可得
,可得![]() ,從而可知
,從而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可設
,可設![]() ,
,
由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的長.
的長.
(1)證明:連接![]() ,如圖1.
,如圖1.
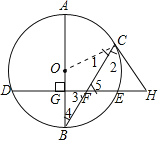
∵![]() 是
是![]() 的切線,
的切線,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)求解思路如下:
思路一:連接![]() ,如圖2.
,如圖2.
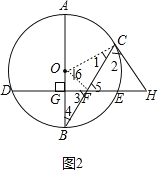
①![]() 過圓心且點
過圓心且點![]() 是
是![]() 的中點,由垂徑定理可得
的中點,由垂徑定理可得![]() ,
,![]() ;
;
②由![]() 與
與![]() 互余,
互余,![]() 與
與![]() 互余可得
互余可得![]() ,從而可知
,從而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可設
,可設![]() ,
,![]() ,由勾股定理,得
,由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的長.
的長.
思路二:連接![]() ,如圖3.
,如圖3.
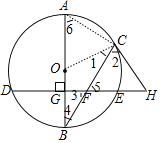
①由![]() 是
是![]() 的直徑,可得
的直徑,可得![]() 是直角三角形,知
是直角三角形,知![]() 與
與![]() 互余,
互余,
又![]() 可知
可知![]() 與
與![]() 互余,得
互余,得![]() ;
;
②由![]() ,
,![]() ,可得
,可得![]() ,從而可知
,從而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可設
,可設![]() ,
,
由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的長.
的長.


科目:初中數學 來源: 題型:
【題目】某班為了解學生一學期做義工的時間情況,對全班50名學生進行調查,按做義工的時間![]() (單位:小時),將學生分成五類:
(單位:小時),將學生分成五類: ![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),繪制成尚不完整的條形統計圖如圖11.
),繪制成尚不完整的條形統計圖如圖11.

根據以上信息,解答下列問題:
(1)![]() 類學生有 人,補全條形統計圖;
類學生有 人,補全條形統計圖;
(2)![]() 類學生人數占被調查總人數的 %;
類學生人數占被調查總人數的 %;
(3)從該班做義工時間在![]() 的學生中任選2人,求這2人做義工時間都在
的學生中任選2人,求這2人做義工時間都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“新冠肺炎”肆虐,無數抗疫英雄涌現,以下四位抗疫英雄是鐘南山、李蘭娟、李文亮、張定宇(依次記為![]() ).為讓同學們了解四位的事跡,老師設計如下活動:取四張完全相同的卡片,分別寫上
).為讓同學們了解四位的事跡,老師設計如下活動:取四張完全相同的卡片,分別寫上![]() 四個標號,然后背面朝上放置,攪勻后每個同學從中隨機抽取一張,記下標號后放回,老師要求每位同學依據抽到的卡片上的標號查找相應抗疫英雄的資料,并做成小報.
四個標號,然后背面朝上放置,攪勻后每個同學從中隨機抽取一張,記下標號后放回,老師要求每位同學依據抽到的卡片上的標號查找相應抗疫英雄的資料,并做成小報.

(1)班長在四種卡片中隨機抽到標號為![]() 的概率為_______.
的概率為_______.
(2)平平和安安兩位同學抽到的卡片是不同英雄的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點到直線的距離即為點到直線的垂線段的長.

(1)如圖1,取點M(1,0),則點M到直線l:y=![]() x﹣1的距離為多少?
x﹣1的距離為多少?
(2)如圖2,點P是反比例函數y=![]() 在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=
在第一象限上的一個點,過點P分別作PM⊥x軸,作PN⊥y軸,記P到直線MN的距離為d0,問是否存在點P,使d0=![]() ?若存在,求出點P的坐標,若不存在,請說明理由.
?若存在,求出點P的坐標,若不存在,請說明理由.
(3)如圖3,若直線y=kx+m與拋物線y=x2﹣4x相交于x軸上方兩點A、B(A在B的左邊).且∠AOB=90°,求點P(2,0)到直線y=kx+m的距離最大時,直線y=kx+m的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是“已知底邊及底邊上的高線作等腰三角形”的尺規作圖過程.
已知:線段![]() .求作:等腰
.求作:等腰![]() ,使
,使![]() ,
,![]() 邊上的高為
邊上的高為![]() .作法:如圖,(1)作線段
.作法:如圖,(1)作線段![]() ;(2)作線段
;(2)作線段![]() 的垂直平分線
的垂直平分線![]() 交
交![]() 于點
于點![]() ;(3)在射線
;(3)在射線![]() 上順次截取線段
上順次截取線段![]() ,連接
,連接![]() .所以
.所以![]() 即為所求作的等腰三角形.
即為所求作的等腰三角形.
請回答:得到![]() 是等腰三角形的依據是:
是等腰三角形的依據是:
①_____:
②_____.
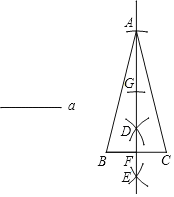
查看答案和解析>>
科目:初中數學 來源: 題型:
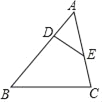
【題目】如圖,已知△ABC,D、E分別在邊AB、AC上,下列條件中,不能確定△ADE∽△ACB的是( )
A. ∠AED=∠B B. ∠BDE+∠C=180°
C. ADBC=ACDE D. ADAB=AEAC
查看答案和解析>>
科目:初中數學 來源: 題型:
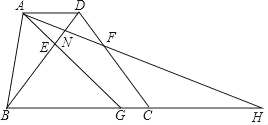
【題目】如圖,在梯形ABCD中,AD∥BC,BC=18,DB=DC=15,點E、F分別在線段BD、CD上,DE=DF=5.AE的延長線交邊BC于點G,AF交BD于點N、其延長線交BC的延長線于點H.
(1)求證:BG=CH;
(2)設AD=x,△ADN的面積為y,求y關于x的函數解析式,并寫出它的定義域;
(3)聯結FG,當△HFG與△ADN相似時,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
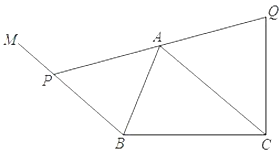
【題目】已知:如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .過點
.過點![]() 作
作![]() ,動點
,動點![]() 在射線
在射線![]() 上(點
上(點![]() 不與
不與![]() 重合),聯結
重合),聯結![]() 并延長到點
并延長到點![]() ,使
,使![]() .
.
(1)求![]() 的面積;
的面積;
(2)設![]() ,
,![]() ,求
,求![]() 關于
關于![]() 的函數解析式,并寫出
的函數解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)連接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若拋物線![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() ,直線
,直線![]() 經過點
經過點![]() ,
,![]() .
.
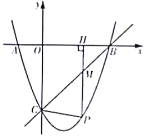
(1)求拋物線的解析式;
(2)點![]() 是直線
是直線![]() 下方拋物線上一動點,過點
下方拋物線上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
①線段![]() 是否有最大值?如果有,求出最大值;如果沒有,請說明理由;
是否有最大值?如果有,求出最大值;如果沒有,請說明理由;
②在點![]() 運動的過程中,是否存在點
運動的過程中,是否存在點![]() ,恰好使
,恰好使![]() 是以
是以![]() 為腰的等腰三角形?如果存在,請直接寫出點
為腰的等腰三角形?如果存在,請直接寫出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com