
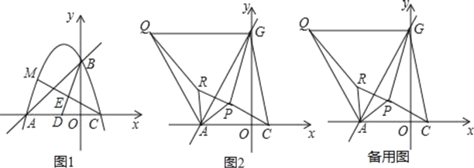
【題目】已知拋物線y=﹣x2﹣2x+3交x軸于點A、C(點A在點C左側),交y軸于點B.
(1)求A,B,C三點坐標;
(2)如圖1,點D為AC中點,點E在線段BD上,且BE=2DE,連接CE并延長交拋物線于點M,求點M坐標;
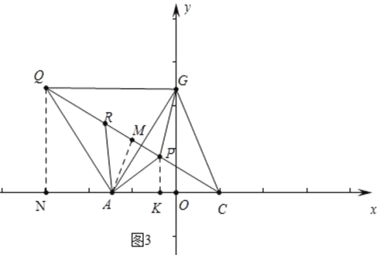
(3)如圖2,將直線AB繞點A按逆時針方向旋轉15°后交y軸于點G,連接CG,點P為△ACG內一點,連接PA、PC、PG,分別以AP、AG為邊,在它們的左側作等邊△APR和等邊△AGQ,求PA+PC+PG的最小值,并求當PA+PC+PG取得最小值時點P的坐標(直接寫出結果即可).
【答案】(1)A(﹣3,0),C(1,0),B(0,3);(2)M(﹣![]() ,
,![]() );(3)2
);(3)2![]() ,P(﹣
,P(﹣![]() ,
,![]() ).
).
【解析】
(1)拋物線![]() 中,令
中,令![]() ,可得A,C坐標;當x=0時,可得B的坐標;
,可得A,C坐標;當x=0時,可得B的坐標;
(2)首先利用A、C坐標,求出D的坐標,根據BE=2ED,求出點E坐標,求出直線CE,利用方程組求交點坐標M即可;
(3)先證明△QAR≌△GAP即可得出QR=PG,進而得到PA+PC+PG=PR+PC+QR,可得當Q,R,P,C共線時,PA+PC+PG的值最小,即為線段QC的長,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K,利用勾股定理求得QC的長,再求出AM,CM,利用等邊三角形性質求出AP、PM、PC,由此即可解決問題.
解:(1)拋物線y=﹣x2﹣2x+3中,令y=﹣x2﹣2x+3=0,可得x1=1,x2=﹣3,
∴A(﹣3,0),C(1,0),
當x=0時,y=3,
∴B(0,3);
(2)∵點D為AC中點,A(﹣3,0),C(1,0),
∴D(﹣1,0),
∵BE=2DE,B(0,3),
∴E(﹣![]() ,1),
,1),
設直線CE為y=kx+b,把C(1,0),E(﹣![]() ,1)代入,可得
,1)代入,可得
 ,解得
,解得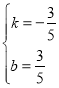 ,
,
∴直線CE為y=﹣![]() x+
x+![]() ,
,
解方程組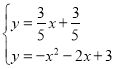 ,可得
,可得![]() 或
或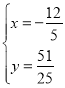 ,
,
∵M在第二象限,
∴M(﹣![]() ,
,![]() );
);
(3)∵△APR和△AGQ是等邊三角形,
∴AP=AR=PR,AQ=AG,∠QAG=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,
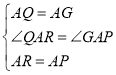 ,
,
∴△QAR≌△GAP(SAS),
∴QR=PG,
∴PA+PC+PG=PR+PC+QR,
∴當Q,R,P,C共線時,PA+PC+PG的值最小,即為線段QC的長,
如圖3,作QN⊥OA于N,作AM⊥CQ于M,作PK⊥CN于K,
依題意得∠GAO=45°+15°=60°,AO=3,
∴AG=GQ=QA=6,∠AGO=30°,OG=3![]() ,
,
∵∠AGQ=60°,
∴∠QGO=90°,
∴Q(﹣6,3![]() ),
),
在Rt△QNC中,QN=3![]() ,CN=6+1=7,
,CN=6+1=7,
∴QC=![]() =2
=2![]() ,即PA+PC+PG的最小值為2
,即PA+PC+PG的最小值為2![]() ,
,
∴sin∠ACM=![]() =
= ![]() ,
,
∴AM=![]() =
= ![]() ,
,
∵△APR是等邊三角形,
∴∠APM=60°,PM=![]() AM,MC=
AM,MC=![]() =
= ![]() ,
,
∴PC=CM﹣PM=![]() ,
,
∵sin∠PCN=![]() =
= ![]() ,cos∠PCN=
,cos∠PCN=![]() =
= ![]() ,
,
∴PK=![]() ,CK=
,CK=![]() ,
,
∴OK=![]() ,
,
∴P(﹣![]() ,
,![]() ).
).


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:
【題目】如圖,將△ABC放在每個小正方形的邊長為1的網格中,點A,B,C均落在格點上.
(1)△ABC的面積等于____;
(2)請在如圖所示的網格中,用無刻度的直尺,過點A畫一條直線,交BC于點D,使△ABD的面積等于△ADC面積的2倍,并簡要說明畫圖的方法(不要求證明).___

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,且
的直徑,且![]() ,點
,點![]() 為
為![]() 外一點,且
外一點,且![]() ,
,![]() 分別切
分別切![]() 于點
于點![]() 、
、![]() 兩點.
兩點.![]() 與
與![]() 的延長線交于點
的延長線交于點![]() .
.
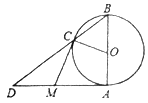
(1)求證:![]() ;
;
(2)填空
①當![]() ________時,四邊形
________時,四邊形![]() 是正方形.
是正方形.
②當![]() _________時,
_________時,![]() 為等邊三角形.
為等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題情境)
我們知道若一個矩形是的周長固定,當相鄰兩邊相等,即為正方形時,它的面積最大.反過來,若一個矩形的面積固定,它的周長是否會有最值呢?
(探究方法)
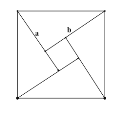
用兩個直角邊分別為![]() ,
,![]() 的4個全等的直角三角形可以拼成一個正方形。若
的4個全等的直角三角形可以拼成一個正方形。若![]() ,可以拼成如圖所示的正方形,從而得到
,可以拼成如圖所示的正方形,從而得到![]() ,即
,即![]() ;當
;當![]() 時,中間小正方形收縮為1個點,此時正方形的面積等于4個直角三角形面積的和.即
時,中間小正方形收縮為1個點,此時正方形的面積等于4個直角三角形面積的和.即![]() .于是我們可以得到結論:
.于是我們可以得到結論:![]() ,
,![]() 為正數,總有
為正數,總有![]() ,當且僅當
,當且僅當![]() 時,代數式
時,代數式![]() 取得最小值
取得最小值![]() .另外,我們也可以通過代數式運算得到類似上面的結論:
.另外,我們也可以通過代數式運算得到類似上面的結論:
∵![]() ,∴
,∴![]() ,
,![]()
∴對于任意實數![]() ,
,![]() 總有
總有![]() ,且當
,且當![]() 時,代數式
時,代數式![]() 取最小值
取最小值![]() .
.
使得上面的方法,對于正數![]() ,
,![]() ,試比較
,試比較![]() 和
和![]() 的大小關系.
的大小關系.
(類比應用)
利用上面所得到的結論完成填空
(1)當![]() 時,代數式
時,代數式![]() 有最 值為 .
有最 值為 .
(2)當![]() 時,代數式
時,代數式![]() 有最 值為 .
有最 值為 .
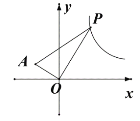
(3)如圖,已知![]() 是反比例函數
是反比例函數![]() 圖象上任意一動點,
圖象上任意一動點,![]() ,
,![]() ,試求
,試求![]() 的最小面積.
的最小面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
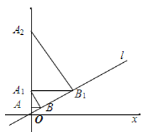
【題目】如圖,已知直線l:y=![]() x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續下去,則點A2020的坐標為______________.
x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續下去,則點A2020的坐標為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC頂點的坐標分別為A(﹣3,3),B(﹣5,2),C(﹣1,1).
(1)以點C為位似中心,作出△ABC的位似圖形△A1B1C,使其位似比為1:2,且ABC位于點C的異側,并表示出點A1的坐標.
(2)作出△ABC繞點C順時針旋轉90°后的圖形△A2B2C.
(3)在(2)的條件下求出點B經過的路徑長(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
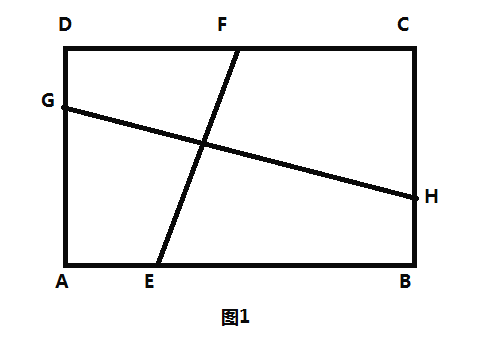
【題目】如圖1,在矩形![]() 中,
中,![]() 點
點![]() 分別在邊
分別在邊![]() 上,點
上,點![]() 分別在邊
分別在邊![]() 上,且
上,且![]() .
.
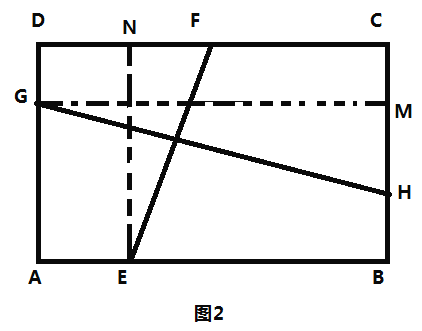
![]() 如圖2,過點
如圖2,過點![]() 作
作![]() 于點
于點![]() 過點
過點![]() 作
作![]() 于點
于點![]() 可知四邊形
可知四邊形![]() 四邊形
四邊形![]() 四邊形
四邊形![]() 四邊形
四邊形![]() 都是矩形,即
都是矩形,即![]()
![]() ,通過證明
,通過證明![]() 可求得
可求得![]() 的值為_ .
的值為_ .
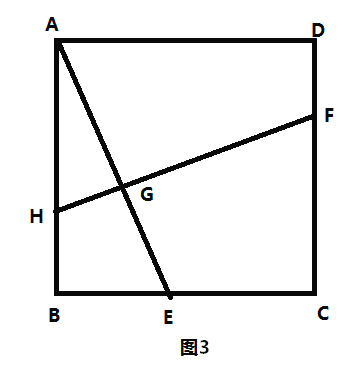
![]() 如圖3,在正方形
如圖3,在正方形![]() 中,點
中,點![]() 分別在邊
分別在邊![]() 上,
上,![]() 于點
于點![]() ,則
,則![]() 的值為 .
的值為 .
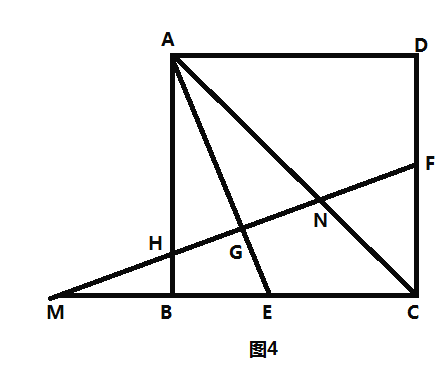
![]() 如圖4,在
如圖4,在![]() 的條件下,延長
的條件下,延長![]() 交
交![]() 的延長線于點
的延長線于點![]() 連接
連接![]() 交
交![]() 于點
于點![]() .若
.若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com