
【題目】如圖,在△ABC中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,且
,且![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)當直線![]() 繞點
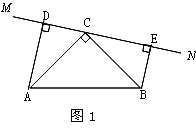
繞點![]() 旋轉到圖1的位置時,
旋轉到圖1的位置時,
①求證:△ADC≌△CEB.
②求證:DE=AD+BE.
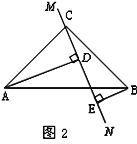
(2)當直線![]() 繞點
繞點![]() 旋轉到圖2的位置時,判斷
旋轉到圖2的位置時,判斷![]() 和
和![]() 的關系,并說明理由.
的關系,并說明理由.
【答案】(1)①見解析;②見解析;(2)△ADC≌△CEB;理由見解析
【解析】
(1)①要證△ADC≌△CEB,已知一直角∠ADC=∠CEB=90°和一邊AC=CB對應相等,由題意根據同角的余角相等,可得另一內角∠ECB=∠DAC,再由AAS即可判定;
②由①得出AD=CE,BE=CD,而DE=CD+CE,故DE=AD+BE;
(2)同理,根據上一小題的解題思路,易得△ADC≌△CEB.
(1)①∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
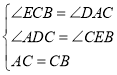
∴△ADC≌△CEB(AAS)
②∵△ADC≌△CEB
∴AD=CE,BE=CD
又∵DE=CD+CE
∴DE=AD+BE
(2)△ADC≌△CEB;
∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
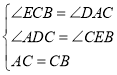
∴△ADC≌△CEB(AAS)


科目:初中數學 來源: 題型:
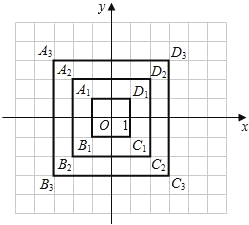
【題目】在平面直角坐標系中,橫坐標、縱坐標都為整數的點稱為整點.請你觀察圖中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每個正方形四條邊上的整點的個數.按此規律推算出正方形A10B10C10D10四條邊上的整點共有______個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某股民上星期五買進某公司股票1000股,每股27元,下表為本周內每日該股票的漲跌情況(單位:元)(周六、周日休盤)
星期 | 一 | 二 | 三 | 四 | 五 |
每股 漲跌 | +4 | +4.5 | -1 | -1.5 | -4 |
(1)星期五收盤時,每股是多少元?
(2)本周內最高價是每股多少元?最低價是每股多少元?
(3)已知該股民買進股票時付了0.15%的手續費,賣出時需付成交額0.15%的手續費和0.1%的交易稅,若該股民在星期五收盤前將全部股票賣出,他的收益情況如何?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知坐標平面內的三個點![]() ,
,![]() ,
,![]() ,把
,把![]() 向下平移
向下平移![]() 個單位再向右平移
個單位再向右平移![]() 個單位后得
個單位后得![]() .
.

(1)畫出平移后的圖形,直接寫出![]() ,
,![]() ,
,![]() 三個對應點
三個對應點![]() ,
,![]() ,
,![]() 的坐標;
的坐標;
(2)求![]() 的面積。
的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
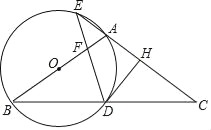
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作圓O,分別交BC于點D,交CA的延長線于點E,過點D作DH⊥AC于點H,連接DE交線段OA于點F.
(1)求證:DH是圓O的切線;
(2)若A為EH的中點,求![]() 的值;
的值;
(3)若EA=EF=1,求圓O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點 A、B 在數軸上分別表示有理數 a、b,A、B 兩點之間的距離表示為 AB, 在數軸上 A、B 兩點之間的距離 AB=|a﹣b|.
![]()
請用上面的知識解答下面的問題:
(1)數軸上表示 1 和 5 的兩點之間的距離是 ,數軸上表示﹣2 和﹣4 的 兩點之間的距離是 ,數軸上表示 1 和﹣3 的兩點之間的距離是 ;
(2)數軸上表示 x 和﹣1 的兩點 A 和 B 之間的距離是 ,如果|AB|=2, 那么 x 為 ;
(3)|x+1|+|x﹣2|取最小值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
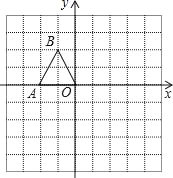
【題目】如圖,在邊長均為1的小正方形網格紙中,△OAB的頂點O,A,B均在格點上,且O是直角坐標系的原點,點A在x軸上.
(1)以O為位似中心,將△OAB放大,使得放大后的△OA1B1,與△OAB對應線段的比為2:1,畫出△OA1B1,(所畫△OA1B1與△OAB在原點兩側);
(2)直接寫出點A1、B1的坐標_____;
(3)直接寫出tan∠OA1B1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:求若干個相同的有理數(均不等于0)的除法運算叫做除方,如![]() ,
,![]() 等,類比有理數的乘方,我們把
等,類比有理數的乘方,我們把![]() 記作
記作![]() ,讀作“2的圈3次方”,把
,讀作“2的圈3次方”,把![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 記作
記作![]() ,讀作“
,讀作“![]() 的圈
的圈![]() 次方”,關于除方,下列說法錯誤的是( )
次方”,關于除方,下列說法錯誤的是( )
A.任何非零數的圈2次方都等于1
B.對于任何正整數![]() ,
,![]()
C.![]()
D.負數的圈奇次方結果是負數,負數的圈偶次方結果是正數.
查看答案和解析>>
科目:初中數學 來源: 題型:
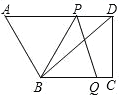
【題目】如圖,在四邊形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.動點P從點D出發,沿射線DA的方向,在射線DA上以每秒2兩個單位長的速度運動,動點Q從點C出發,在線段CB上以每秒1個單位長的速度向點B運動,點P、Q分別從點D,C同時出發,當點Q運動到點B時,點P隨之停止運動.設運動的時間為t(秒).
,BC=4,DC=3,AD=6.動點P從點D出發,沿射線DA的方向,在射線DA上以每秒2兩個單位長的速度運動,動點Q從點C出發,在線段CB上以每秒1個單位長的速度向點B運動,點P、Q分別從點D,C同時出發,當點Q運動到點B時,點P隨之停止運動.設運動的時間為t(秒).
(1)設![]() 的面積為
的面積為![]() ,直接寫出
,直接寫出![]() 與
與![]() 之間的函數關系式是____________(不寫取值范圍).
之間的函數關系式是____________(不寫取值范圍).
(2)當B,P,Q三點為頂點的三角形是等腰三角形時,求出此時![]() 的值.
的值.
(3)當線段PQ與線段AB相交于點O,且2OA=OB時,直接寫出![]() =_____________.
=_____________.
(4)是否存在時刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com