
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+2ax+c交x軸于A,B兩點,交y軸于點C(0,3),tan∠OAC=![]() .
.
(1)求拋物線的解析式;
(2)點H是線段AC上任意一點,過H作直線HN⊥x軸于點N,交拋物線于點P,求線段PH的最大值;

【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)
x+3;(2)![]()
【解析】(1)由點C的坐標以及tan∠OAC=![]() .可得出點A的坐標,結合點A、C的坐標利用待定系數法即可求出拋物線的解析式;
.可得出點A的坐標,結合點A、C的坐標利用待定系數法即可求出拋物線的解析式;
(2)設直線AC的解析式為y=kx+b,由點A、C的解析式利用待定系數法即可求出直線AC的解析式,設N(x,0)(-4<x<0),可找出H、P的坐標,由此即可得出PH關于x的解析式,利用配方法即二次函數的性質即可求出最值.
解:(1)∵C(0,3),
∴OC=3,
∵tan∠OAC=![]() ,
,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得![]() ,
,
解得: 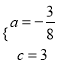 ,
,
∴拋物線的解析式為y=﹣![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)設直線AC的解析式為y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ![]() ,
,
解得: 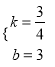 ,
,
∴直線AC的解析式為y=![]() x+3.
x+3.
設N(x,0)(﹣4<x<0),
則H(x, ![]() x+3),P(x,﹣
x+3),P(x,﹣![]() x2﹣
x2﹣![]() x+3),
x+3),
∴PH=﹣![]() x2﹣
x2﹣![]() x+3﹣(
x+3﹣(![]() x+3)=﹣
x+3)=﹣![]() x2﹣
x2﹣![]() x=﹣
x=﹣![]() (x+2)2+
(x+2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴PH有最大值,
即當x=﹣2時,PH取最大值,最大值為![]() .
.


科目:初中數學 來源: 題型:
【題目】根據要求完成畫圖或作答:
如圖所示,已知點![]() 、
、![]() 、
、![]() 是網格紙上的三個格點.
是網格紙上的三個格點.

(1)畫射線![]() ,畫線段
,畫線段![]() ,過點
,過點![]() 畫
畫![]() 的平行線
的平行線![]() ;
;
(2)過點![]() 畫直線
畫直線![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,則點
,則點![]() 到
到![]() 的距離就是線段_________的長度.
的距離就是線段_________的長度.
(3)線段![]() _______線段
_______線段![]() (填“
(填“![]() ”或“
”或“![]() ”),理由是_____________.
”),理由是_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸的正半軸上.若點
軸的正半軸上.若點![]() ,
,![]() 在線段
在線段![]() 上,且
上,且![]() 為某個一邊與
為某個一邊與![]() 軸平行的矩形的對角線,則稱這個矩形為點
軸平行的矩形的對角線,則稱這個矩形為點![]() 、
、![]() 的“涵矩形”.下圖為點
的“涵矩形”.下圖為點![]() ,
,![]() 的“涵矩形”的示意圖.
的“涵矩形”的示意圖.
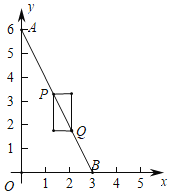
(1)點![]() 的坐標為
的坐標為![]() .
.
①若點![]() 的橫坐標為
的橫坐標為![]() ,點
,點![]() 與點
與點![]() 重合,則點
重合,則點![]() 、
、![]() 的“涵矩形”的周長為__________.
的“涵矩形”的周長為__________.
②若點![]() ,
,![]() 的“涵矩形”的周長為
的“涵矩形”的周長為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,則點
,則點![]() ,
,![]() ,
,![]() 中,能夠成為點
中,能夠成為點![]() 、
、![]() 的“涵矩形”的頂點的是_________.
的“涵矩形”的頂點的是_________.
(2)四邊形![]() 是點
是點![]() 、
、![]() 的“涵矩形”,點
的“涵矩形”,點![]() 在
在![]() 的內部,且它是正方形.
的內部,且它是正方形.
①當正方形![]() 的周長為
的周長為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() 時,求點的坐標.
時,求點的坐標.
②當正方形![]() 的對角線長度為
的對角線長度為![]() 時,連結
時,連結![]() .直接寫出線段
.直接寫出線段![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蕪湖市擬建立了一個學生身份識別系統.利用圖 1 的二維碼可以進行身份識別,圖2是某個學生的識別圖案,黑色小正方形表示 1,白色小正方形表示 0.將第一行數字從左到 右依次記為a,b,c,d,那么可以轉換為該生所在班級序號,其序號為a×23+b×22+c×21+d×20,如圖2第一行數字從左到右依次為 0,1,0,1,序號為0×23+1×22+0×21+1×20=5,表示該生為5班學生,請問,表示10班學生的識別圖案是( )

A. B.
B.
C. D.
D.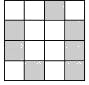
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小紅星期天從家里出發騎車去舅舅家做客,當她騎了一段路時,想起要買個禮物送給表弟,于是又折回到剛經過的一家商店,買好禮物后又繼續騎車去舅舅家,以下是她本次去舅舅家所用的時間與路程的關系式示意圖.根據圖中提供的信息回答下列問題:
(1)小紅家到舅舅家的路程是______米,小紅在商店停留了______分鐘;
(2)在整個去舅舅家的途中哪個時間段小紅騎車速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小紅一共行駛了多少米?一共用了多少分鐘?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A點坐標為(3,3),將△ABC 先向下平移4個單位得△A'B'C',再將△A'B'C'繞點O逆時針旋轉180°得△A'B'C'.
(1)請你畫出△A'B'C'和△A'B'C';
(2)點A'的坐標為 ;
(3)△ABC和△A'B'C'關于某個點中心對稱,這個點的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
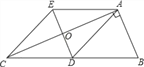
【題目】如圖,在Rt△ABC中,AD是邊BC上的中線,過點A作AE∥BC,過點D作DE∥AB,DE與AC、AE分別交于點O、點E,連結EC.
(1)求證:AD=EC;
(2)求證:四邊形ADCE是菱形;
(3)若AB=AO,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀對人成長的影響是巨大的,一本好書往往能改變人的一生,每年的4月23日被聯合國教科文組織確定為“世界讀書日”.藍天中學為了解八年級學生本學期的課外閱讀情況,隨機抽查部分學生對其課外閱讀量進行統計分析,繪制成兩幅不完整的統計圖.根據圖示信息,解答下列問題:
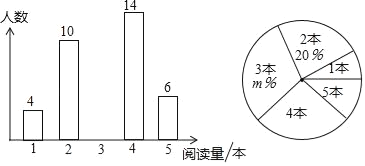
(1)求被抽查學生人數,課外閱讀量的眾數,扇形統計圖中m的值;并將條形統計圖補充完整;
(2)若規定:本學期閱讀3本以上(含3本)課外書籍者為完成目標,據此估計該校600名學生中能完成此目標的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以矩形ABCD兩對角線的交點O為原點建立平面直角坐標系,且x軸過BC中點,y軸過CD中點,y=![]() x﹣2與邊AB、BC分別交于點E、F.若AB=10,BC=3,則△EBF的面積是( )
x﹣2與邊AB、BC分別交于點E、F.若AB=10,BC=3,則△EBF的面積是( )
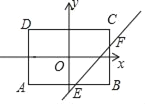
A. 4B. 5C. 6D. 7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com