
【題目】如圖,在四邊形ABCD中,AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,則∠DAB的度數是______°.
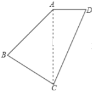
【答案】135°
【解析】
由已知可得AB=BC,從而可求得∠BAC的度數.設AB=2x ,通過計算證明AC2+AD2=CD2,從而證得ΔACD是直角三角形,即可得到∠DAC=90°,從而求得∠DAB的度數.
解:∵AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,
∴AB=BC,
∴∠BAC=∠ACB=45°,
∴設AB=2x,則BC=2x,CD=3x,DA=x,
∴AC2=AB2+BC2=(2x)2+(2x)2=8x2
又CD2-AD2=(3x)2-x2=8x2
∴AC2= CD2-AD2
∵AC2+AD2=CD2
∴ΔACD是直角三角形,
∴∠DAC=90°,
∴∠DAB=45°+90°=135°.
故答案是:135°.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,點A與原點重合,點B在y軸的正半軸上,點D在x軸的負半軸上,將正方形ABCD繞點A逆時針旋轉30°至正方形AB'C′D′的位置,B'C′與CD相交于點M,則點M的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)圖象如圖所示,下列結論:①abc<0;②2a﹣b<0;③b2>(a+c)2;④點(﹣3,y1),(1,y2)都在拋物線上,則有y1>y2.其中正確的結論有( )
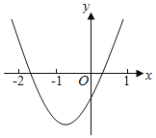
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B繞點B順時針旋轉180°,得到△BP2C;把△BP2C繞點C順時針旋轉180°,得到△CP3D,依此類推,則旋轉第2017次后,得到的等腰直角三角形的直角頂點P2018的坐標為( )
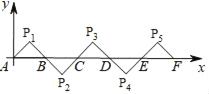
A. (4030,1) B. (4029,﹣1)
C. (4033,1) D. (4035,﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
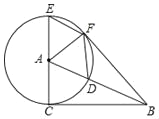
【題目】在Rt△ABC中,∠ACB=90°,以點A為圓心,AC為半徑,作⊙A交AB于點D,交CA的延長線于點E,過點E作AB的平行線EF交⊙A于點F,連接AF、BF、DF
(1)求證:BF是⊙A的切線.
(2)當∠CAB等于多少度時,四邊形ADFE為菱形?請給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王明同學隨機抽查某市![]() 個小區所得到的綠化率情況,結果如下表:
個小區所得到的綠化率情況,結果如下表:
小區綠化率 |
|
|
|
|
小區個數 |
|
|
|
|
則關于這![]() 個小區的綠化率情況,下列說法錯誤的是( )
個小區的綠化率情況,下列說法錯誤的是( )
A. 極差是13% B. 眾數是25% C. 中位數是25% D. 平均數是26.2%
查看答案和解析>>
科目:初中數學 來源: 題型:
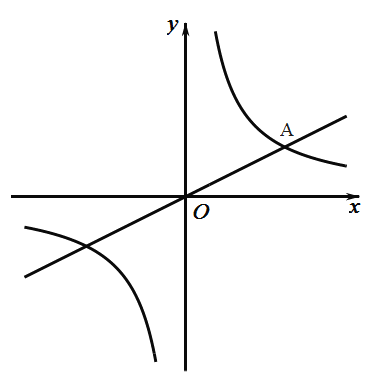
【題目】如圖,已知直線![]() 與雙曲線
與雙曲線![]() 在第一象限交于
在第一象限交于![]() 點,且點
點,且點![]() 的橫坐標為4,點
的橫坐標為4,點![]() 在雙曲線上.
在雙曲線上.
(1)求雙曲線的函數解析式;
(2)若點![]() 的縱坐標為8,試判斷
的縱坐標為8,試判斷![]() 形狀,并說明理由.
形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店將進價為8元的商品按每件10元售出,每天可售出200件,現在采取提高商品售價減少銷售量的辦法增加利潤,如果這種商品每件的銷售價每提高1元,其每天的銷售量就減少20件.
(1)當售價定為12元時,每天可售出________件;
(2)要使每天利潤達到640元,則每件售價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
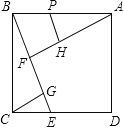
【題目】如圖,在正方形ABCD中,過B作一直線與CD相交于點E,過A作AF垂直BE于點F,過C作CG垂直BE于點G,在FA上截取FH=FB,再過H作HP垂直AF交AB于P.若CG=3.則△CGE與四邊形BFHP的面積之和為 _________ .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com