
【題目】如圖,一次函數y=k1x+b與反比例函數y=![]() 相交于A(﹣1,2),B(2,m)兩點,與y軸相交于點C.
相交于A(﹣1,2),B(2,m)兩點,與y軸相交于點C.
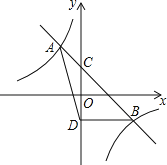
(1)求k1、k2、m的值;
(2)若點D與點C關于x軸對稱,求△ABD的面積;
(3)若M(x1,y1)、N(x2,y2)是反比例函數y=![]() 圖象上的兩點,且x1<x2時,y1>y2,指出點M、N各位于坐標系的哪個象限,并簡要說明理由.
圖象上的兩點,且x1<x2時,y1>y2,指出點M、N各位于坐標系的哪個象限,并簡要說明理由.
【答案】(1)k1=﹣1,k2=﹣2,m=﹣1;(2)3;(3)點M位于第二象限,N位于第四象限.
【解析】
試題分析:(1)把A的坐標代入y=![]() 即可求得k2,得到反比例函數的解析式,再把B(2,m)代入反比例函數的解析式即可求得m的值,然后根據待定系數法即可求得k1;
即可求得k2,得到反比例函數的解析式,再把B(2,m)代入反比例函數的解析式即可求得m的值,然后根據待定系數法即可求得k1;
(2)根據一次函數的解析式求得點C的坐標,根據題意求得D的坐標,從而求得DB∥x軸,BD=2,然后根據三角形,、面積公式求得即可;
(3)根據反比例函數的性質即可判斷.
解:(1)∵比例函數y=![]() 經過A(﹣1,2),
經過A(﹣1,2),
∴k2=﹣y=![]() 經1×2=﹣2,
經1×2=﹣2,
∴比例函數為y=﹣![]() ,
,
∵B(2,m)在比例函數y=﹣![]() 的圖象上,
的圖象上,
∴m=﹣![]() =﹣1,
=﹣1,
∴B(2,﹣1),
∵直線y=k1x+b經過A(﹣1,2),B(2,﹣1),
∴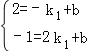 ,解得k1=﹣1,b=1,
,解得k1=﹣1,b=1,
(2)由直線y=﹣x+1可知C(0,1),
∵點D與點C關于x軸對稱,
∴D(0,﹣1),
∵B(2,﹣1),
∴BD∥x軸,BD=2,
∴△ABD的面積=![]() ×2×(2+1)=3;
×2×(2+1)=3;
(3)點M位于第二象限,N位于第四象限,
∵k2=﹣2<0,圖象位于二、四象限,在每個象限內,y隨x的增大而增大,
∴如果M(x1,y1)、N(x2,y2)位于同一象限,有且x1<x2時,則y1<y2,
∴M(x1,y1)、N(x2,y2)位于不同的象限,
∵x1<x2,
∴點M位于第二象限,N位于第四象限.


科目:初中數學 來源: 題型:
【題目】近年來,我國多個城市遭遇霧霾天氣,空氣中可吸入顆粒(又稱PM2.5)濃度升高,為應對空氣污染,小強家購買了空氣凈化器,該裝置可隨時顯示室內PM2.5的濃度,并在PM2.5濃度超過正常值25(mg/m3)時吸收PM2.5以凈化空氣.隨著空氣變化的圖象(如圖),請根據圖象,解答下列問題:
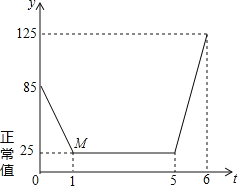
(1)寫出題中的變量;
(2)寫出點M的實際意義;
(3)求第1小時內,y與t的一次函數表達式;
(4)已知第5﹣6小時是小強媽媽做晚餐的時間,廚房內油煙導致PM2.5濃度升高.若該凈化器吸收PM2.5的速度始終不變,則第6小時之后,預計經過多長時間室內PM2.5濃度可恢復正常?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級教師在講“解直角三角形”一節時,帶領一個小組登上學校教學樓上的一個平臺,測量與學校毗鄰的一生活小區的一棟居民樓AB的高度,平臺C距離地面D高10米,在C處測得居民樓樓底B的俯角為22.5°,樓頂端A的仰角為60°,測完后,記錄好數據,回到教師,將示意圖畫在黑板上,如圖所示,要求全班學生按示意圖,求出居民樓AB的高度.(最后結果精確到0.1)(參考數據:tan22.5°=![]() ﹣1,
﹣1,![]() =1.73,
=1.73,![]() =1.41)
=1.41)
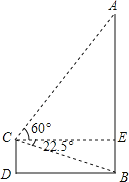
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解決后面的問題。
材料:我們知道,n個相同的因數a相乘![]() 可記為an,如23=8,此時,3叫做以2為底8的對數,記為log28(即log28=3)
可記為an,如23=8,此時,3叫做以2為底8的對數,記為log28(即log28=3)
一般地,若an=b (a>0且a≠1,b>0),則n叫做以a為底b的對數,記為logab(即logab=n).如34=81,則4叫做以3為底81的對數,記為log381(即log381=4)
(1)計算以下各對數的值:log24= ,log216= ,log264= .
(2)觀察(1)中三數4、16、64之間滿足怎樣的關系式?log24、log216、log264之間又滿足怎樣的關系式?
(3)根據(2)的結果,我們可以歸納出:logaM+logaN=logaM N (a>0且a≠1,M>0,N>0),請你根據冪的運算法則:am=an+m以及對數的定義證明該結論。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com