
【題目】解方程與不等式(組)
(1)![]() +1<x﹣3;
+1<x﹣3;
(2)![]() +3=
+3= ![]() ;
;
(3)解不等式組 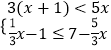 .
.
【答案】
(1)解x﹣5+2<2x﹣6
x>3:
(2)解:1+3(x﹣2)=x﹣1
2x=4
x=2
經檢驗,x=2時原方程的增根
(3)解:由①可得:x> ![]()
由②可得:x≤4
∴不等式組的解集為: ![]() <x≤4
<x≤4
【解析】(1)根據不等式的解法即可求出答案.(2)根據分式方程的解法即可求出答案.(3)根據不等式組的解法即可求出答案.
【考點精析】認真審題,首先需要了解去分母法(先約后乘公分母,整式方程轉化出.特殊情況可換元,去掉分母是出路.求得解后要驗根,原留增舍別含糊),還要掌握一元一次不等式的解法(步驟:①去分母;②去括號;③移項;④合并同類項; ⑤系數化為1(特別要注意不等號方向改變的問題))的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】阜陽某企業今年1月份產值為a萬元,2月份比1月份減少了10%,預計3月份比2月份增加15%.則3月份的產值將達到( )
A.(a﹣10%)(a+15%)萬元
B.(a﹣10%+15%)萬元
C.a(1﹣10%)(1+15%)萬元
D.a(1﹣10%+15%)萬元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在x軸上有兩點A(m,0),B(n,0)(n>m>0),分別過點A,B作x軸的垂
線交拋物線y=x2于點C,D,直線OC交直線BD于點E,直線OD交直線AC于點F.點E,F的縱坐標分別為yE,yF.
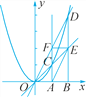
(1)特例探究(填空):
當m=1,n=2時,yE=____,yF=____;
當m=3,n=5時,yE=____,yF=____.
(2)歸納證明:對任意m,n(n>m>0),猜想yE與yF的大小關系,并證明你的猜想.
(3)拓展應用:連結EF,AE,當S四邊形OFEB=3S△OFE時,直接寫出m與n的關系及四邊形OFEA的形狀.
查看答案和解析>>
科目:初中數學 來源: 題型:
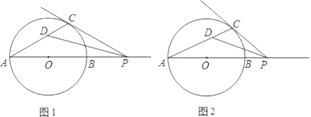
【題目】已知AB為⊙O的直徑,P為AB延長線上的任意一點,過點P作⊙O的切線,切點為C,∠APC的平分線PD與AC交于點D.
(1)如圖1,若∠CPA恰好等于30°,求∠CDP的度數;
(2)如圖2,若點P位于(1)中不同的位置,(1)的結論是否仍然成立?說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com