【題目】如圖，B、A、F三點在同一直線上，（1）AD∥BC，（2）∠B＝∠C，（3）AD平分∠EAC.
請你用其中兩個作為條件，另一個作為結論，構造一個真命題，并證明.
己知:______________________________________________________.
求證:______________________________________________________.
證明:
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，已知點B的坐標為（6，4）．
（1）請用直尺（不帶刻度）和圓規作一條直線AC，它與x軸和y軸的正半軸分別交于點A和點C，且使∠ABC=90°，△ABC與△AOC的面積相等．（作圖不必寫作法，但要保留作圖痕跡．）
（2）問：（1）中這樣的直線AC是否唯一？若唯一，請說明理由；若不唯一，請在圖中畫出所有這樣的直線AC，并寫出與之對應的函數表達式．
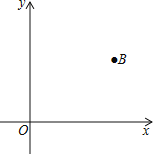
查看答案和解析>>
科目：初中數學 來源： 題型：
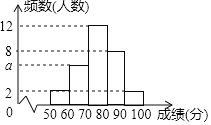
【題目】為了解某次“小學生書法比賽”的成績情況，隨機抽取了30名學生的成績進行統計，并將統計情況繪成如圖所示的頻數分布直方圖，己知成績x（單位：分）均滿足“50≤x＜100”．根據圖中信息回答下列問題：
（1）圖中a的值為 ；
（2）若要繪制該樣本的扇形統計圖，則成績x在“70≤x＜80”所對應扇形的圓心角度數為 度；
（3）此次比賽共有300名學生參加，若將“x≥80”的成績記為“優秀”，則獲得“優秀“的學生大約有 人：
（4）在這些抽查的樣本中，小明的成績為92分，若從成績在“50≤x＜60”和“90≤x＜100”的學生中任選2人，請用列表或畫樹狀圖的方法，求小明被選中的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線AB、CD相交于點O．已知∠BOD＝75°，OE把∠AOC分成兩個角，且∠AOE：∠EOC＝2：3．
（1）求∠AOE的度數；
（2）若OF平分∠BOE，問：OB是∠DOF的平分線嗎？試說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為選拔一名選手參加“美麗邵陽，我為家鄉做代言”主題演講比賽，經研究，按圖所示的項目和權數對選拔賽參賽選手進行考評（因排版原因統計圖不完整）．下表是李明、張華在選拔賽中的得分情況：
項目 選手 | 服裝 | 普通話 | 主題 | 演講技巧 |
李明 | 85 | 70 | 80 | 85 |
張華 | 90 | 75 | 75 | 80 |
結合以上信息，回答下列問題：
（1）求服裝項目的權數及普通話項目對應扇形的圓心角大小；
（2）求李明在選拔賽中四個項目所得分數的眾數和中位數；
（3）根據你所學的知識，幫助學校在李明、張華兩人中選擇一人參加“美麗邵陽，我為家鄉做代言”主題演講比賽，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC中，∠BAC=100°．
（1）若∠ABC和∠ACB的角平分線交于點O，如圖1所示，試求∠BOC的大小；
（2）若∠ABC和∠ACB的三等分線（即將一個角平均分成三等分的射線）相交于O，O1，如圖2所示，試求∠BOC的大小；
（3）如此類推，若∠ABC和∠ACB的n等分線自下而上依次相交于O，O1，O2…，如圖3所示，試探求∠BOC的大小與n的關系，并判斷當∠BOC=170°時，是幾等分線的交線所成的角．
查看答案和解析>>
科目：初中數學 來源： 題型：
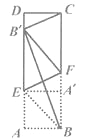
【題目】如圖，將矩形紙片ABCD折疊，使點A與BC邊上的點A′重合，折痕為BE，再沿過點E的直線折疊，使點B與AD邊上的點 B重合，折痕為EF，連結
,
．
，則
的值為________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀并解答問題：
數學大師的名題與方程
歐拉是18世紀瑞士著名的數學大師．他的一生都致力于數學各個領域的研究，并取得非凡的成就．在他所著的《代數學入門》一書中就曾經出現過好幾道和遺產分配有關的數學問題．他構思這些問題的初衷，正是為了強化方程解題的適用和便利．
請用適當的方法解答下面問題：
父親死后，四個兒子按下述方式分了他的財產：老大拿了財產的一半少3000英鎊：老二拿了財產的
少1000英鎊；老三拿了恰好是財產的
；老四拿了財產的
加上600英鎊．問整個財產有多少？每個兒子各分了多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
