
【題目】海靜中學開展以“我最喜愛的職業”為主題的調查活動,圍繞“在演員、教師、醫生、律師、公務員共五類職業中,你最喜愛哪一類?(必選且只選一類)”的問題,在全校范圍內隨機抽取部分學生進行問卷調查,將調查結果整理后繪制成如圖所示的不完整的統計圖,請你根據圖中提供的信息回答下列問題: 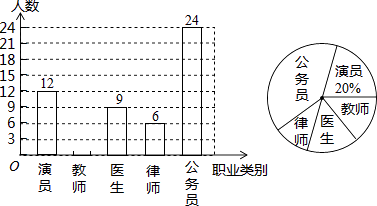
(1)本次調查共抽取了多少名學生?
(2)求在被調查的學生中,最喜愛教師職業的人數,并補全條形統計圖;
(3)若海靜中學共有1500名學生,請你估計該中學最喜愛律師職業的學生有多少名?
【答案】
(1)解:12÷20%=60,
答:共調查了60名學生.
(2)解:60﹣12﹣9﹣6﹣24=9,
答:最喜愛的教師職業人數為9人.如圖所示: 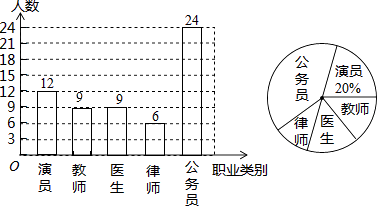
(3)解: ![]() ×1500=150(名)
×1500=150(名)
答:該中學最喜愛律師職業的學生有150名.
【解析】(1)用條形圖中演員的數量結合扇形圖中演員的百分比可以求出總調查學生數;(2)用總調查數減去其他幾個職業類別就可以得到最喜愛教師職業的人數;(3)利用調查學生中最喜愛律師職業的學生百分比可求出該中學中的相應人數.
【考點精析】利用扇形統計圖和條形統計圖對題目進行判斷即可得到答案,需要熟知能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況;能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況.


科目:初中數學 來源: 題型:
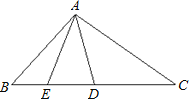
【題目】已知:如圖,D是△ABC的邊BC上的一點,且CD=AB,∠BDA=∠BAD,AE是△ABD的中線.
⑴若∠B=60°,求∠C的值;
⑵求證:AD是∠EAC的平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
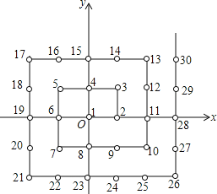
【題目】某班共有52名同學,在校廣播操比賽中排成方隊,先把每位同學都進行編號,然后把各自的位置固定下來,如圖,在平面直角坐標系中,每個自然數都對應著一個坐標.例如1的對應點是原點![]() ,3的對應點是
,3的對應點是![]() ,16的對應點是
,16的對應點是![]() .那么最后一名同學的位置對應的坐標是____,全校學生如果排成這樣一個大方陣,編號是2015的學生的對應點的坐標是___.
.那么最后一名同學的位置對應的坐標是____,全校學生如果排成這樣一個大方陣,編號是2015的學生的對應點的坐標是___.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究題:
(1)三條直線相交,最少有__________個交點,最多有__________個交點,分別畫出圖形,并數出圖形中的對頂角和鄰補角的對數;
(2)四條直線相交,最少有__________個交點,最多有__________個交點,分別畫出圖形,并數出圖形中的對頂角和鄰補角的對數;
(3)依次類推,n條直線相交,最少有__________個交點,最多有__________個交點,對頂角有__________對,鄰補角有__________對.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖a是一個長為2m、寬為2n的長方形,沿圖中實現用剪刀均分成四塊小長方形,然后按圖b的形狀拼成一個正方形.

(1)圖b中,大正方形的邊長是 .陰影部分小正方形的邊長是 ;
(2)觀察圖b,寫出(m+n)2,(m﹣n)2,mn之間的一個等量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和爸爸從家步行去公園,爸爸先出發一直勻速前進,小明后出發,家到公園的距離為2500m,如圖是小明和爸爸所走路程s(m)與步行時間t(min)的函數圖象. 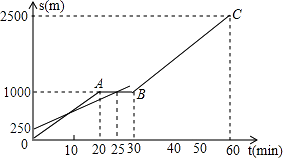
(1)直接寫出小明所走路程s與時間t的函數關系式;
(2)小明出發多少時間與爸爸第三次相遇?
(3)在速度都不變的情況下,小明希望比爸爸早20min到達公園,則小明在步行過程中停留的時間需作怎樣的調整?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某地九年級學生參加消防知識競賽成績(均為整數),從中抽取了1%的同學的競賽成績,整理后繪制了如下的頻數直方圖,請結合圖形解答下列問題:
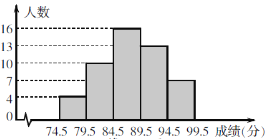
(1)這個問題中的總體是________________;
(2)競賽成績在84.5~89.5分這一小組的頻率是_____________;
(3)若競賽成績在90分以上(含90分)的同學可以獲得獎勵,則估計該地獲得獎勵的九年級學生約有_____人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D為△ABC內一點,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,則BD的長為( )

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
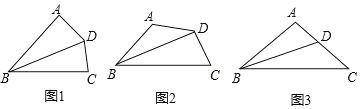
【題目】如圖,在四邊形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如圖,若α=90°,根據教材中一個重要性質直接可得 DA=CD,這個性質是__________.
(2)問題解決:如圖,求證AD=CD;
(3)問題拓展:如圖,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求證:BD+AD=BC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com