
【題目】如圖,正方形ABCD中,AB=3cm,以B為圓心,1cm為半徑畫圓,點P是⊙B上一個動點,連接AP,并將AP繞點A逆時針旋轉(zhuǎn)90°至AP',連接BP',在點P移動的過程中,BP'長度的取值范圍是_____cm.

【答案】(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1).
+1).
【解析】
通過畫圖發(fā)現(xiàn),點P′的運(yùn)動路線為以D為圓心,以1為半徑的圓,可知:當(dāng)P′在對角線BD上時,BP′最小,先證明△PAB≌△P′AD,則P′D=PB=1,再利用勾股定理求對角線BD的長,則得出BP′的長.
如圖,當(dāng)P′在對角線BD上時,BP′最小;當(dāng)P′在對角線BD的延長線上時,BP′最大.
連接BP,
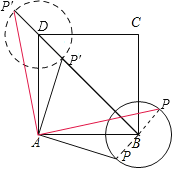
①當(dāng)P′在對角線BD上時,
由旋轉(zhuǎn)得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四邊形ABCD為正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=![]() =3
=3![]() ,
,
∴BP′=BD-P′D=3![]() -1,
-1,
即BP′長度的最小值為(3![]() -1)cm.
-1)cm.
②當(dāng)P′在對角線BD的延長線上時,
同理可得BD=![]() =3
=3![]() ,
,
∴BP′=BD+P′D=3![]() +1,
+1,
即BP′長度的最大值為(3![]() +1)cm.
+1)cm.
∴BP'長度的取值范圍是(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1)cm
+1)cm
故答案為:(3![]() -1)cm≤BP≤(3
-1)cm≤BP≤(3![]() +1).
+1).


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點P為拋物線![]() 為常數(shù),
為常數(shù),![]() )上任意一點,將拋物線繞頂點G逆時針旋轉(zhuǎn)90°后得到的圖象與
)上任意一點,將拋物線繞頂點G逆時針旋轉(zhuǎn)90°后得到的圖象與![]() 軸交于A、B兩點(點A在點B的上方),點Q為點P旋轉(zhuǎn)后的對應(yīng)點.
軸交于A、B兩點(點A在點B的上方),點Q為點P旋轉(zhuǎn)后的對應(yīng)點.
(1)拋物線![]() 的對稱軸是直線________,當(dāng)m=2時,點P的橫坐標(biāo)為4時,點Q的坐標(biāo)為_________;
的對稱軸是直線________,當(dāng)m=2時,點P的橫坐標(biāo)為4時,點Q的坐標(biāo)為_________;
(2)設(shè)點Q![]() 請你用含m,
請你用含m,![]() 的代數(shù)式表示
的代數(shù)式表示![]() 則
則![]() ________;
________;
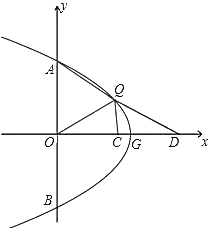
(3)如圖,點Q在第一象限,點D在![]() 軸的正半軸上,點C為OD的中點,QO平分∠AQC,當(dāng)AQ=2QC,QD=
軸的正半軸上,點C為OD的中點,QO平分∠AQC,當(dāng)AQ=2QC,QD=![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:點P(m,4)在反比例函數(shù)y=﹣![]() 的圖象上,正比例函數(shù)的圖象經(jīng)過點P和點Q(6,n).
的圖象上,正比例函數(shù)的圖象經(jīng)過點P和點Q(6,n).
(1)求正比例函數(shù)的解析式;
(2)求P、Q兩點之間的距離.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
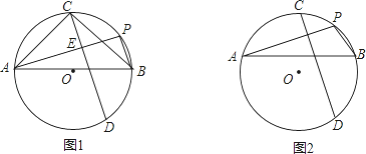
【題目】(1)如圖1,PA、PB是⊙O的兩條弦,AB為直徑,C為![]() 的中點,弦CD⊥PA于點E,寫出AB與AC的數(shù)量關(guān)系,并證明;
的中點,弦CD⊥PA于點E,寫出AB與AC的數(shù)量關(guān)系,并證明;
(2)如圖2,PA、PB是⊙O的兩條弦,AB為弦,C為劣弧![]() 的中點,弦CD⊥PA于E,寫出AE、PE與PB的數(shù)量關(guān)系,并證明.
的中點,弦CD⊥PA于E,寫出AE、PE與PB的數(shù)量關(guān)系,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】列方程解應(yīng)用題:
某玩具廠生產(chǎn)一種玩具,按照控制固定成本降價促銷的原則,使生產(chǎn)的玩具能夠及時售出,據(jù)市場調(diào)查:每個玩具按![]() 元銷售時,每天可銷售
元銷售時,每天可銷售![]() 個;若銷售單價每降低元,每天可多售出
個;若銷售單價每降低元,每天可多售出![]() 個.已知每個玩具的固定成本為
個.已知每個玩具的固定成本為![]() 元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤
元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤![]() 元?
元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
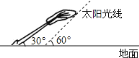
【題目】如圖,太陽光線與地面成![]() 角,一棵傾斜的大樹與地面成
角,一棵傾斜的大樹與地面成![]() 角,這時測得大樹在地面上的影長約為
角,這時測得大樹在地面上的影長約為![]() ,則大樹的長約為________
,則大樹的長約為________![]() (保留兩個有效數(shù)字,下列數(shù)據(jù)供選用:
(保留兩個有效數(shù)字,下列數(shù)據(jù)供選用:![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點C在⊙O上,過點C的直線與AB的延長線交于點P,AC=PC,∠COB=2∠PCB.
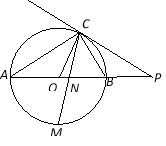
(1)求證:PC是⊙O的切線;
(2)求證:BC=AB;
(3)點M是弧AB的中點,CM交AB于點N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形OABC在平面直角坐標(biāo)系xOy中,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=4,OC=3,若拋物線的頂點在BC邊上,且拋物線經(jīng)過O,A兩點,直線AC交拋物線于點D.

(1)求拋物線的解析式;
(2)求點D的坐標(biāo);
(3)若點M在拋物線上,點N在x軸上,是否存在以A,D,M,N為頂點的四邊形是平行四邊形?若存在,求出點N的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com