
【題目】如圖,已知點A,B在半徑為1的⊙O上,∠AOB=60°,延長OB至C,過點C作直線OA的垂線記為l,則下列說法正確的是( )

A.當BC等于0.5時,l與⊙O相離
B.當BC等于2時,l與⊙O相切
C.當BC等于1時,l與⊙O相交
D.當BC不為1時,l與⊙O不相切
【答案】D
【解析】
試題分析:根據圓心到直線的距離大于半徑,直線與圓相離,圓心到直線的距離小于半徑,直線與圓相交;圓心到直線的距離等于半徑,直線與圓相切,可得
A、∵BC=0.5,∴OC=OB+CB=1.5;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=0.5<1,∴l與⊙O相交,故A錯誤;
OC=0.5<1,∴l與⊙O相交,故A錯誤;
B、∵BC=2,∴OC=OB+CB=3;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=1.5>1,∴l與⊙O相離,故B錯誤;
OC=1.5>1,∴l與⊙O相離,故B錯誤;
C、∵BC=1,∴OC=OB+CB=2;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC=1,∴l與⊙O相切,故C錯誤;
OC=1,∴l與⊙O相切,故C錯誤;
D、∵BC≠1,∴OC=OB+CB≠2;∵∠AOB=60°,∴∠ACO=30°,AO=![]() OC≠1,∴l與⊙O不相切,故D正確;
OC≠1,∴l與⊙O不相切,故D正確;
故選:D.


科目:初中數學 來源: 題型:
【題目】 “囧”(jiong)是近時期網絡流行語,像一個人臉郁悶的神情.如圖所示,一張邊長為20的正方形的紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分).設剪去的小長方形長和寬分別為x、y,剪去的兩個小直角三角形的兩直角邊長也分別為x、y.
(1)用含有x、y的代數式表示右圖中“囧”的面積;
(2)當![]() 時,求此時“囧”的面積.
時,求此時“囧”的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A、B在數軸上分別表示有理數a、b,A、B兩點之間的距離表示為AB,則在數軸上A、B兩點之間的距離AB=|a﹣b|.
所以式子|x﹣2|的幾何意義是數軸上表示x的點與表示2的點之間的距離.借助于數軸回答下列問題:
①數軸上表示2和5兩點之間的距離是 , 數軸上表示1和﹣3的兩點之間的距離是 .
②數軸上表示x和﹣2的兩點之間的距離表示為 .
③數軸上表示x的點到表示1的點的距離與它到表示﹣3的點的距離之和可表示為:|x﹣1|+|x+3|.則|x﹣1|+|x+3|的最小值是 .
④若|x﹣3|+|x+1|=8,則x=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點A出發沿AD向點D勻速運動,速度是1cm/s,過點P作PE∥AC交DC于點E,同時,點Q從點C出發沿CB方向,在射線CB上勻速運動,速度是2cm/s,連接PQ、QE,PQ與AC交與點F,設運動時間為t(s)(0<t<8).
(1)當t為何值時,四邊形PFCE是平行四邊形;
(2)設△PQE的面積為s(cm2),求s與t之間的函數關系式;
(3)是否存在某一時刻t,使得△PQE的面積為矩形ABCD面積的![]() ;
;
(4)是否存在某一時刻t,使得點E在線段PQ的垂直平分線上.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①、②、③中,點E、D分別是正△ABC、正四邊形ABCM、正五邊形ABCMN中以C點為頂點的相鄰兩邊上的點,且BE=CD,DB交AE于P點.
(1)求圖①中,∠APD的度數為_______;(2)圖②中,∠APD的度數為_________,
(3)圖③中,∠APD的度數為_______;
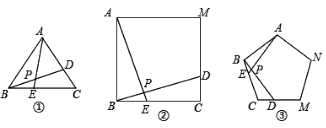
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com