
【題目】已知:△ABC為等邊三角形
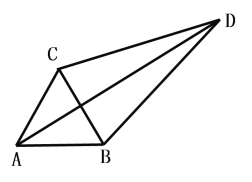
(1)若D為△ABC外一點(diǎn),滿(mǎn)足∠CDB=30,求證:![]()
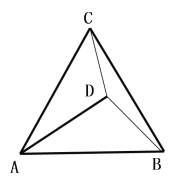
(2)若D為△ABC內(nèi)一點(diǎn),DC=3,DB=4,DA=5,求∠CDB的度數(shù)
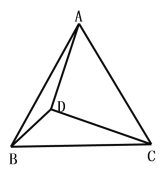
(3)若D為△ABC內(nèi)一點(diǎn),DA=4,DB=![]() ,DC=
,DC=![]() 則AB= (直接寫(xiě)出答案)
則AB= (直接寫(xiě)出答案)
【答案】(1)詳見(jiàn)解析;(2)150;(3)![]()
【解析】
(1)以BD為邊作等邊△BDQ,易證△ABD≌△CBQ得AD=CQ再證∠CDQ=90得![]() .
.
(2) 把△ACD繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°得到△BCQ,如圖,連接DQ,根據(jù)旋轉(zhuǎn)的性質(zhì)得∠DCQ=60°,CD=CQ=3,QB=AD=5,則可判斷△CDQ為等邊三角形,所以DQ=4,∠BDE=60°,再利用勾股定理的逆定理證明△BDQ為直角三角形,∠QDB=90°,從而得到∠CDB=150°.
(3)同②可得∠ADB=150°,解構(gòu)造30°直角三角形即可求出AB.
(1)證明:以BD為邊作等邊△BDQ,連接QC,
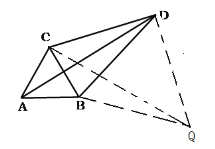
∵:△ABC、△BDQ都是等邊三角形,
∴∠ABC=∠DBQ=∠BDQ=60°,BA=BC,BD=BQ,
∴∠ABD=∠CBQ,
在△ABD和△CBQ中
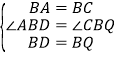 ,
,
∴△ABD≌△CBQ(SAS),
∴AD=CQ
又∵∠CDB=30,
∴∠CDQ=90
∴![]()
∴![]()
(2)解: 把△ACD繞點(diǎn)C逆時(shí)針旋轉(zhuǎn)60°得到△BCQ,如圖,連接DQ,
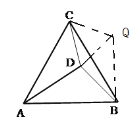
∵△ABC為等邊三角形,
∴BA=BC,∠ABC=60°,
∴∠QCD=60°,CD=CQ=3,QB=AD=5,
∴△CDQ為等邊三角形,
∴DE=4,∠DQC=60°,
在△BDQ中,∵DQ=3,BD=4,BQ=5,
∴DQ2+BD2=BQ2,
∴△DEC為直角三角形,∠QDC=90°,
∴∠CDB=60°+90°=150°.
(3)AB=![]()
解:把△ACD繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)60°得到△BCQ,如圖,連接DQ,
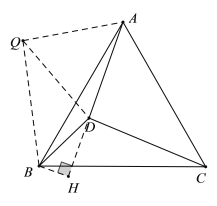
同可得②BQ= DC=![]() ,AD=AQ=DQ=4,DB=
,AD=AQ=DQ=4,DB=![]() ,
,
∴DQ2+BD2=BQ2,∠ADB=150°,
過(guò)B點(diǎn)作BH垂直AD,交AD延長(zhǎng)線(xiàn)于H,
∴∠BDH=30°,
∴BH=![]() BD=
BD=![]() ,DH=3,
,DH=3,
∴AH=AD+DH=3+4=7,
∴AB=![]() =
=![]() =
=![]()
故答案為:![]()


 培優(yōu)口算題卡系列答案
培優(yōu)口算題卡系列答案 開(kāi)心口算題卡系列答案
開(kāi)心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF翻折,點(diǎn)A恰好落在BC邊的A′處,若AB= ![]() ,∠EFA=60°,則四邊形A′B′EF的周長(zhǎng)是( )
,∠EFA=60°,則四邊形A′B′EF的周長(zhǎng)是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,分別是可活動(dòng)的菱形和平行四邊形學(xué)具,已知平行四邊形較短的邊與菱形的邊長(zhǎng)相等.
(1)在一次數(shù)學(xué)活動(dòng)中,某小組學(xué)生將菱形的一邊與平行四邊形較短邊重合,擺拼成如圖1所示的圖形,AF經(jīng)過(guò)點(diǎn)C,連接DE交AF于點(diǎn)M,觀(guān)察發(fā)現(xiàn):點(diǎn)M是DE的中點(diǎn).
下面是兩位學(xué)生有代表性的證明思路:
思路1:不需作輔助線(xiàn),直接證三角形全等;
思路2:不證三角形全等,連接BD交AF于點(diǎn)H.…
請(qǐng)參考上面的思路,證明點(diǎn)M是DE的中點(diǎn)(只需用一種方法證明);
(2)如圖2,在(1)的前提下,當(dāng)∠ABE=135°時(shí),延長(zhǎng)AD、EF交于點(diǎn)N,求![]() 的值;
的值;
(3)在(2)的條件下,若![]() =k(k為大于
=k(k為大于![]() 的常數(shù)),直接用含k的代數(shù)式表示
的常數(shù)),直接用含k的代數(shù)式表示![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
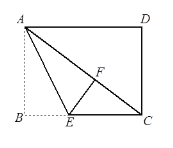
【題目】如圖,已知在長(zhǎng)方形ABCD中,將△ABE沿著AE折疊至△AEF的位置,點(diǎn)F在對(duì)角線(xiàn)AC上,若BE=3,EC=5,則線(xiàn)段CD的長(zhǎng)是__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
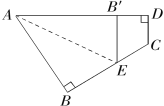
【題目】如圖所示,一個(gè)四邊形紙片ABCD,∠B=∠D=![]() ,把紙片按如圖所示折疊,使點(diǎn)B落在AD邊上的B′點(diǎn),AE是折痕.
,把紙片按如圖所示折疊,使點(diǎn)B落在AD邊上的B′點(diǎn),AE是折痕.
(1)試判斷B′E與DC的位置關(guān)系;并說(shuō)明理由.
(2)如果∠C=![]() ,求∠AEB的度數(shù).
,求∠AEB的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,O為坐標(biāo)原點(diǎn),點(diǎn)A(1,5)和點(diǎn)B(m,1)均在反比例函數(shù)y=![]() 圖象上.
圖象上.
(1)求m,k的值;
(2)設(shè)直線(xiàn)AB與x軸交于點(diǎn)C,求△AOC的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知四邊形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD與BC平行嗎?試寫(xiě)出推理過(guò)程;
(2)求∠DAC和∠EAD的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算、求解:
(1)用代人消元法解方程組:![]() ;
;
(2)加減消元法解方程組:![]() ;
;
(3)計(jì)算:![]() ;
;
(4)解不等式組 ,并把解集在數(shù)軸上表示出來(lái),
,并把解集在數(shù)軸上表示出來(lái),
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線(xiàn)![]() ,其中
,其中![]() 是常數(shù),該拋物線(xiàn)的對(duì)稱(chēng)軸為直線(xiàn)
是常數(shù),該拋物線(xiàn)的對(duì)稱(chēng)軸為直線(xiàn)![]() .
.
(![]() )求該拋物線(xiàn)的函數(shù)解析式.
)求該拋物線(xiàn)的函數(shù)解析式.
(![]() )把該拋物線(xiàn)沿
)把該拋物線(xiàn)沿![]() 軸向上平移多少個(gè)單位后,得到的拋物線(xiàn)與
軸向上平移多少個(gè)單位后,得到的拋物線(xiàn)與![]() 軸只有一個(gè)公共點(diǎn).
軸只有一個(gè)公共點(diǎn).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com