
【題目】已知拋物線![]() ,其中
,其中![]() 是常數,該拋物線的對稱軸為直線
是常數,該拋物線的對稱軸為直線![]() .
.
(![]() )求該拋物線的函數解析式.
)求該拋物線的函數解析式.
(![]() )把該拋物線沿
)把該拋物線沿![]() 軸向上平移多少個單位后,得到的拋物線與
軸向上平移多少個單位后,得到的拋物線與![]() 軸只有一個公共點.
軸只有一個公共點.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:
(1)把拋物線的解析式整理為一般形式,由此可得到其對稱軸的表達式,結合對稱軸是直線![]() 即可解出“m”的值,從而可求得其解析式;
即可解出“m”的值,從而可求得其解析式;
(2)設把該拋物線向上平移![]() 個單位長度后與
個單位長度后與![]() 軸只有一個公共點,由此可得新的解析式的表達式,再由“△=
軸只有一個公共點,由此可得新的解析式的表達式,再由“△=![]() ”即可求得
”即可求得![]() 的值.
的值.
試題解析:
(1)∵![]() 可化為:
可化為: ![]() ,
,
∴該拋物線的對稱軸為直線: ![]() ,
,
又∵該拋物線的對稱軸為:直線![]() ,
,
∴![]() ,解得:
,解得: ![]() ,
,
∴拋物線的解析式為: ![]() ;
;
(![]() )設原拋物線向上平移
)設原拋物線向上平移![]() 個單位后與
個單位后與![]() 軸只有1個公共點,則平移后拋物線解析式為:
軸只有1個公共點,則平移后拋物線解析式為:
![]() ,
,
∵它與![]() 軸只有一個公共點,
軸只有一個公共點,
∴![]() ,解得:
,解得: ![]() ,
,
即,將該拋物線向上平移![]() 個單位長度后,新拋物線與
個單位長度后,新拋物線與![]() 軸只有1個公共點.
軸只有1個公共點.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
【題目】已知:△ABC為等邊三角形
(1)若D為△ABC外一點,滿足∠CDB=30,求證:![]()
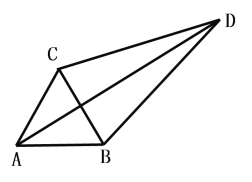
(2)若D為△ABC內一點,DC=3,DB=4,DA=5,求∠CDB的度數
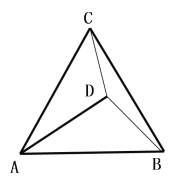
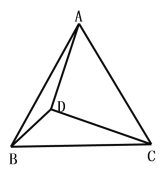
(3)若D為△ABC內一點,DA=4,DB=![]() ,DC=
,DC=![]() 則AB= (直接寫出答案)
則AB= (直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E 、F ,連結BD 、DP ,BD與CF相交于點H. 給出下列結論:①△BDE ∽△DPE;② ![]() ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④![]() . 其中正確的是( ).
. 其中正確的是( ).
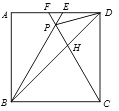
A. ①②③④ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中,調查方式選擇最合理的是![]()
![]()
A. 為了解安徽省中學生的課外閱讀情況,選擇全面調查
B. 調查七年級某班學生打網絡游戲的情況,選擇抽樣調查
C. 為確保長征六號遙二火箭成功發射,應對零部件進行全面調查
D. 為了解一批袋裝食品是否含有防腐劑,選擇全面調查
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王剪了兩張直角三角形紙片,進行了如下的操作:

操作一:如圖1,將Rt△ABC沿某條直線折疊,使斜邊的兩個端點A與B重合,折痕為DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周長為 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度數為 ;
操作二:如圖2,小王拿出另一張Rt△ABC紙片,將直角邊AC沿直線AD折疊,使它落在斜邊AB上,且與AE重合,若AC=9cm,BC=12cm,請求出CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),公路上有A、B、C三個車站,一輛汽車從A站以速度v1勻速駛向B站,到達B站后不停留,以速度v2勻速駛向C站,汽車行駛路程y(千米)與行駛時間x(小時)之間的函數圖象如圖(2)所示.

(1)當汽車在A、B兩站之間勻速行駛時,求y與x之間的函數關系式及自變量的取值范圍;
(2)求出v2的值;
(3)若汽車在某一段路程內剛好用50分鐘行駛了90千米,求這段路程開始時x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .在同一平面直線坐標系中
.在同一平面直線坐標系中
(![]() )若函數
)若函數![]() 的圖象過點
的圖象過點![]() ,函數
,函數![]() 的圖象過點
的圖象過點![]() ,求
,求![]() ,
, ![]() 的值.
的值.
(![]() )若函數
)若函數![]() 的圖象經過
的圖象經過![]() 的頂點.
的頂點.
①求證: ![]() .
.
②當![]() 時,比較
時,比較![]() ,
, ![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
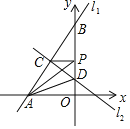
【題目】已知直線![]() :
:![]() 與直線
與直線![]() :
:![]() 都經過
都經過![]() ,直線
,直線![]() 交y軸于點
交y軸于點![]() ,交x軸于點A,直線
,交x軸于點A,直線![]() 交y軸于點D,P為y軸上任意一點,連接PA、PC,有以下說法:①方程組
交y軸于點D,P為y軸上任意一點,連接PA、PC,有以下說法:①方程組 的解為
的解為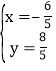 ;②
;②![]() 為直角三角形;③
為直角三角形;③![]() ;④當
;④當![]() 的值最小時,點P的坐標為
的值最小時,點P的坐標為![]() 其中正確的說法個數有
其中正確的說法個數有![]()
![]()
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請將下列證明過程補充完整:
已知:如圖,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求證:AB∥CD.
證明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性質)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com