
【題目】如圖1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,連接CD、AE交于點F.
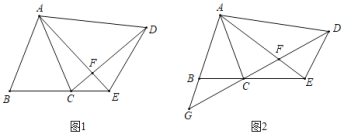
(1)求證:BE=CD.
(2)當∠BAC=∠EAD=30°,AD⊥AB時(如圖2),延長DC、AB交于點G,請直接寫出圖中除△ABC、△ADE以外的等腰三角形.
【答案】(1)見解析;(2)△ACF是等腰三角形,△ADG是等腰三角形,△DEF是等腰三角形,△ECD是等腰三角形.
【解析】
(1)由“SAS”可證△ACD≌△ABE,可得BE=CD;
(2)如圖2,圖形中有四個等腰三角形:分別是①△ACF是等腰三角形,②△ADG是等腰三角形,③△DEF是等腰三角形;④△ECD是等腰三角形;根據已知角的度數依次計算各角的度數,根據兩個角相等的三角形是等腰三角形得出結論.
解:(1)如圖1,∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,且AB=AC,AD=AE,
∴△ACD≌△ABE(SAS)
∴BE=CD;
(2)如圖2,
①∵∠BAC=∠EAD=30°,
∴∠ABC=∠ACB=∠AED=∠ADE=75°,
由(1)得:∠ACD=∠ABC=75°,
∠DCE=∠BAC=30°,
∵AD⊥AB,
∴∠BAD=90°,
∴∠CAE=30°,
∴∠AFC=180°﹣30°﹣75°=75°,
∴∠ACF=∠AFC,
∴△ACF是等腰三角形,
②∵∠BCG=∠DCE=30°,∠ABC=75°,
∴∠G=45°,
在Rt△AGD中,∠ADG=45°,
∴△ADG是等腰三角形,
③∠EDF=75°﹣45°=30°,
∴∠DEF=∠DFE=75°,
∴△DEF是等腰三角形;
④∵∠ECD=∠EDC=30°,
∴△ECD是等腰三角形.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】在如圖的方格中,每個小正方形的邊長都為1,△ABC的頂點均在格點上。在建立平面直角坐標系后,點B的坐標為(-1,2).

(1)把△ABC向下平移8個單位后得到對應的△![]() ,畫出△
,畫出△![]() ,并寫出
,并寫出![]() 坐標;
坐標;
(2)以原點O為對稱中心,畫出與△![]() 關于原點O對稱的△
關于原點O對稱的△![]()
![]()
![]() ,并寫出點
,并寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b與反比例函數y=![]() (m≠0)的圖象交于點A(3,1),且過點B(0,﹣2).
(m≠0)的圖象交于點A(3,1),且過點B(0,﹣2).
(1)求反比例函數和一次函數的表達式;
(2)如果點P是x軸上一點,且△ABP的面積是3,求點P的坐標.
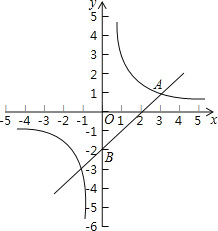
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“垃圾不落地,城市更美麗”.某中學為了了解七年級學生對這一倡議的落實情況,學校安排政教處在七年級學生中隨機抽取了部分學生,并針對學生“是否隨手丟垃圾”這一情況進行了問卷調查,統計結果為:A為從不隨手丟垃圾;B為偶爾隨手丟垃圾;C為經常隨手丟垃圾三項.要求每位被調查的學生必須從以上三項中選一項且只能選一項.現將調查結果繪制成以下來不辜負不完整的統計圖.
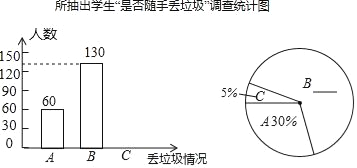
請你根據以上信息,解答下列問題:
(1)補全上面的條形統計圖和扇形統計圖;
(2)所抽取學生“是否隨手丟垃圾”情況的眾數是 ;
(3)若該校七年級共有1500名學生,請你估計該年級學生中“經常隨手丟垃圾”的學生約有多少人?談談你的看法?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知拋物線y=ax2+bx+c的圖像經過點A(0,3)、B(1,0),其對稱軸為直線l:x=2,過點A作AC∥x軸交拋物線于點C,∠AOB的平分線交線段AC于點E,點P是拋物線上的一個動點,設其橫坐標為m.

(1)求拋物線的解析式;
(2)若動點P在直線OE下方的拋物線上,連結PE、PO,當m為何值時,四邊形AOPE面積最大,并求出其最大值;
(3)如圖②,F是拋物線的對稱軸l上的一點,在拋物線上是否存在點P使△POF成為以點P為直角頂點的等腰直角三角形?若存在,直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把平面內一條數軸x繞點O逆時針旋轉角θ(0°<θ<90°)得到另一條數軸y,x軸和y軸構成一個平面斜坐標系.規定:已知點P是平面斜坐標系中任意一點,過點P作y軸的平行線交x軸于點A,過點P作x軸的平行線交y軸于點B,若點A在x軸上對應的實數為a,點B在y軸上對應的實數為b,則稱有序實數對(a,b)為點P的斜坐標.在平面斜坐標系中,若θ=45°,點P的斜坐標為(1,2![]() ),點G的斜坐標為(7,﹣2
),點G的斜坐標為(7,﹣2![]() ),連接PG,則線段PG的長度是_____.
),連接PG,則線段PG的長度是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的周長為36,對角線AC、BD相交于點O,點E是CD的中點,BD=12,則△DOE的周長為( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com