
【題目】如圖,AB是⊙O的直徑,BC是⊙O的切線,切點為B,OC相交于點D,且CD=2,BC=4, 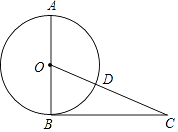
(1)求⊙O的半徑;
(2)連接AD并延長,交BC于點E,取BE的中點F,連接DF,試判斷DF與⊙O的位置關系,并說明理由.
【答案】
(1)解:設⊙O的半徑為R,
∵BC是⊙O的切線,
∴∠OBC=90°,
∴OB2+BC2=OC2,
即R2+42=(R+2)2,
解得:R=3,
即⊙O的半徑為3
(2)解:DF與⊙O相切;理由如下:
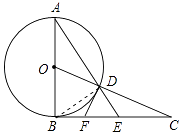
如圖所示:連接BD,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB是⊙O的直徑,
∴∠ADB=90°,
∴∠BDE=90°,
∵F是BE的中點,
∴DF= ![]() BE=BF,
BE=BF,
∴∠DBF=∠BDF,
∵∠DBF+∠OBD=90°,
∴∠BDF+∠ODB=90°,
∴DF⊥OD,
∴DF與⊙O相切.
【解析】(1)設⊙O的半徑為R,由切線的性質得出∠OBC=90°,由勾股定理得出方程,解方程即可;(2)連接BD,由等腰三角形的性質得出∠OBD=∠ODB,由圓周角定理得出∠ADB=90°,求出∠BDE=90°,由直角三角形的性質得出DF= ![]() BE=BF,得出∠DBF=∠BDF,證出∠BDF+∠ODB=90°,即可得出結論.
BE=BF,得出∠DBF=∠BDF,證出∠BDF+∠ODB=90°,即可得出結論.
【考點精析】解答此題的關鍵在于理解切線的性質定理的相關知識,掌握切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑.


 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】如圖,在A地往北60m的B處有一幢房,西80m的C處有一變電設施,在BC的中點D處有古建筑.因施工需要在A處進行一次爆破,為使房、變電設施、古建筑都不遭到破壞,問爆破影響面的半徑應控制在什么范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,ABCD的兩條對角線相交于點O,E是BO的中點.過點B作AC的平行線BF,交CE的延長線于點F,連接AF. 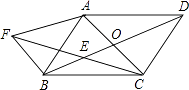
(1)求證:△FBE≌△COE;
(2)將ABCD添加一個條件,使四邊形AFBO是菱形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸為x=1,給出下列結論:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正確的結論是 . (寫出正確命題的序號) 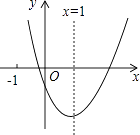
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿對角線BD折疊,使C落在F處,BF交AD于E,則下列結論不一定成立的是( ) 
A.AD=BF
B.△ABE≌FDE
C.sin ![]()
D.△ABE∽△CBD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中點,ED的延長線與CB的延長線交于點F. 
(1)求證:FD2=FBFC;
(2)若G是BC的中點,連接GD,GD與EF垂直嗎?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二孩政策的落實引起了全社會的關注,某校學生數學興趣小組為了了解本校同學對父母生育二孩的態度,在學校抽取了部分同學對父母生育二孩所持的態度進行了問卷調查,調查分別為非常贊同、贊同、無所謂、不贊同等四種態度,現將調查統計結果制成了如圖兩幅統計圖,請結合兩幅統計圖,回答下列問題: 
(1)在這次問卷調查中一共抽取了名學生,a=%;
(2)請補全條形統計圖;
(3)持“不贊同”態度的學生人數的百分比所占扇形的圓心角為度;
(4)若該校有3000名學生,請你估計該校學生對父母生育二孩持“贊同”和“非常贊同”兩種態度的人數之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠CAB=30°,∠C=90°.AD= ![]() AC,AB=8,E是AB上任意一點,F是AC上任意一點,則折線DEFB的最短長度為 .
AC,AB=8,E是AB上任意一點,F是AC上任意一點,則折線DEFB的最短長度為 . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com