
【題目】在平面直角坐標系中,我們定義直線![]() 為拋物線
為拋物線![]() 、b、c為常數,
、b、c為常數,![]() 的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.

已知拋物線![]() 與其“夢想直線”交于A、B兩點
與其“夢想直線”交于A、B兩點![]() 點A在點B的左側
點A在點B的左側![]() ,與x軸負半軸交于點C.
,與x軸負半軸交于點C.
![]() 填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
![]() 如圖,點M為線段CB上一動點,將
如圖,點M為線段CB上一動點,將![]() 以AM所在直線為對稱軸翻折,點C的對稱點為N,若
以AM所在直線為對稱軸翻折,點C的對稱點為N,若![]() 為該拋物線的“夢想三角形”,求點N的坐標;
為該拋物線的“夢想三角形”,求點N的坐標;
![]() 當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)N點坐標為
;(2)N點坐標為![]() 或
或![]() ;(3)
;(3)![]() 、
、![]() 或
或![]() 、
、![]()
【解析】試題分析:(1)由夢想直線的定義可求得其解析式,聯立夢想直線與拋物線解析式可求得A、B的坐標;
(2)當N點在y軸上時,過A作AD⊥y軸于點D,則可知AN=AC,結合A點坐標,則可求得ON的長,可求得N點坐標;當M點在y軸上即M點在原點時,過N作NP⊥x軸于點P,由條件可求得∠NMP=60°,在Rt△NMP中,可求得MP和NP的長,則可求得N點坐標;
(3)當AC為平行四邊形的一邊時,過F作對稱軸的垂線FH,過A作AK⊥x軸于點K,可證△EFH≌△ACK,可求得DF的長,則可求得F點的橫坐標,從而可求得F點坐標,由HE的長可求得E點坐標;當AC為平行四邊形的對角線時,設E(﹣1,t),由A、C的坐標可表示出AC中點,從而可表示出F點的坐標,代入直線AB的解析式可求得t的值,可求得E、F的坐標.
(1)∵拋物線![]() ,∴其夢想直線的解析式為
,∴其夢想直線的解析式為![]() ,聯立夢想直線與拋物線解析式可得:
,聯立夢想直線與拋物線解析式可得: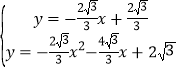 ,解得:
,解得:![]() 或
或![]() ,∴A(﹣2,
,∴A(﹣2,![]() ),B(1,0),故答案為:
),B(1,0),故答案為:![]() ;(﹣2,
;(﹣2,![]() );(1,0);
);(1,0);
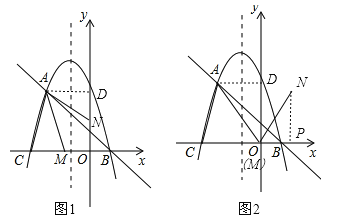
(2)當點N在y軸上時,△AMN為夢想三角形,如圖1,過A作AD⊥y軸于點D,則AD=2,在![]() 中,令y=0可求得x=﹣3或x=1,∴C(﹣3,0),且A(﹣2,
中,令y=0可求得x=﹣3或x=1,∴C(﹣3,0),且A(﹣2,![]() ),∴AC=
),∴AC=![]() =
=![]() ,由翻折的性質可知AN=AC=
,由翻折的性質可知AN=AC=![]() ,在Rt△AND中,由勾股定理可得DN=
,在Rt△AND中,由勾股定理可得DN=![]() =
=![]() =3,∵OD=
=3,∵OD=![]() ,∴ON=
,∴ON=![]() ﹣3或ON=
﹣3或ON=![]() +3,當ON=
+3,當ON=![]() +3時,則MN>OD>CM,與MN=CM矛盾,不合題意,∴N點坐標為(0,
+3時,則MN>OD>CM,與MN=CM矛盾,不合題意,∴N點坐標為(0,![]() ﹣3);
﹣3);
當M點在y軸上時,則M與O重合,過N作NP⊥x軸于點P,如圖2,在Rt△AMD中,AD=2,OD=![]() ,∴tan∠DAM=
,∴tan∠DAM=![]() =
=![]() ,∴∠DAM=60°,∵AD∥x軸,∴∠AMC=∠DAO=60°,又由折疊可知∠NMA=∠AMC=60°,∴∠NMP=60°,且MN=CM=3,∴MP=
,∴∠DAM=60°,∵AD∥x軸,∴∠AMC=∠DAO=60°,又由折疊可知∠NMA=∠AMC=60°,∴∠NMP=60°,且MN=CM=3,∴MP=![]() MN=
MN=![]() ,NP=
,NP=![]() MN=
MN=![]() ,∴此時N點坐標為(
,∴此時N點坐標為(![]() ,
,![]() );
);
綜上可知N點坐標為(0,![]() ﹣3)或(
﹣3)或(![]() ,
,![]() );
);
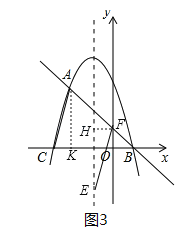
(3)①當AC為平行四邊形的邊時,如圖3,過F作對稱軸的垂線FH,過A作AK⊥x軸于點K,則有AC∥EF且AC=EF,∴∠ACK=∠EFH,在△ACK和△EFH中,∵∠ACK=∠EFH,∠AKC=∠EHF,AC=EF,∴△ACK≌△EFH(AAS),∴FH=CK=1,HE=AK=![]() ,∵拋物線對稱軸為x=﹣1,∴F點的橫坐標為0或﹣2,∵點F在直線AB上,∴當F點橫坐標為0時,則F(0,
,∵拋物線對稱軸為x=﹣1,∴F點的橫坐標為0或﹣2,∵點F在直線AB上,∴當F點橫坐標為0時,則F(0,![]() ),此時點E在直線AB下方,∴E到y軸的距離為EH﹣OF=
),此時點E在直線AB下方,∴E到y軸的距離為EH﹣OF=![]() ﹣
﹣![]() =
=![]() ,即E點縱坐標為﹣
,即E點縱坐標為﹣![]() ,∴E(﹣1,﹣
,∴E(﹣1,﹣![]() );
);
當F點的橫坐標為﹣2時,則F與A重合,不合題意,舍去;
②當AC為平行四邊形的對角線時,∵C(﹣3,0),且A(﹣2,![]() ),∴線段AC的中點坐標為(﹣2.5,
),∴線段AC的中點坐標為(﹣2.5,![]() ),設E(﹣1,t),F(x,y),則x﹣1=2×(﹣2.5),y+t=
),設E(﹣1,t),F(x,y),則x﹣1=2×(﹣2.5),y+t=![]() ,∴x=﹣4,y=
,∴x=﹣4,y=![]() ﹣t,代入直線AB解析式可得
﹣t,代入直線AB解析式可得![]() ﹣t=﹣
﹣t=﹣![]() ×(﹣4)+
×(﹣4)+![]() ,解得t=﹣
,解得t=﹣![]() ,∴E(﹣1,﹣
,∴E(﹣1,﹣![]() ),F(﹣4,
),F(﹣4,![]() );
);
綜上可知存在滿足條件的點F,此時E(﹣1,﹣![]() )、F(0,
)、F(0,![]() )或E(﹣1,﹣
)或E(﹣1,﹣![]() )、F(﹣4,
)、F(﹣4,![]() ).
).


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】某片果園有果樹80棵,現準備多種一些果樹提高果園產量,但是如果多種樹,那么樹之間的距離和每棵樹所受光照就會減少,單棵樹的產量隨之降低,若該果園每棵果樹產果y千克,增種果樹x棵,它們之間的函數關系如圖所示.

(1)求y與x之間的函數解析式;
(2)在投入成本最低的情況下,增種果樹多少棵時,果園可以收獲果實6750千克?
(3)當增種果樹多少棵時,果園的總產量w(千克)最大?最大產量是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,點F在AC延長線上,![]() ,DE是△ABC中位線,如果∠1=30°,DE=2,則四邊形AFED的周長是________
,DE是△ABC中位線,如果∠1=30°,DE=2,則四邊形AFED的周長是________

查看答案和解析>>
科目:初中數學 來源: 題型:
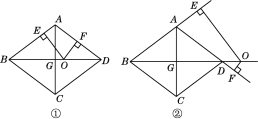
【題目】如圖,在邊長為10的菱形ABCD中,對角線BD=16,對角線AC,BD相交于點G,點O是直線BD上的動點,OE⊥AB于E,OF⊥AD于F.
(1)求對角線AC的長及菱形ABCD的面積.
(2)如圖①,當點O在對角線BD上運動時,OE+OF的值是否發生變化?請說明理由.
(3)如圖②,當點O在對角線BD的延長線上時,OE+OF的值是否發生變化?若不變,請說明理由;若變化,請探究OE,OF之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,點O在AB上,經過點A的⊙O與BC相切于點D,交AB于點E.
(1)求證:AD平分∠BAC;
(2)若CD=1,求圖中陰影部分的面積(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在10×10的正方形網格中,每個小正方形的邊長為1個單位長度.△ABC的頂點都在正方形網格的格點上,且通過兩次平移(沿網格線方向作上下或左右平移)后得到△A′B′C′,點C的對應點是直線上的格點C′.

(1)畫出△A′B′C′.
(2)△ABC兩次共平移了___個單位長度。
(3)試在直線上畫出點P,使得由點A′、B′、C′、P四點圍成的四邊形的面積為9.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以△ABC的AB、AC為邊分別作正方形ADEB、ACGF,連接DC、BF:
(1)CD與BF相等嗎?請說明理由;
(2)CD與BF互相垂直嗎?請說明理由;
(3)利用旋轉的觀點,在此題中,△ADC可看成由哪個三角形繞哪點旋轉多少角度得到的?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙C過原點O,且與兩坐標軸分別交于點A、B,點A的坐標為(0,2),M是第三象限內⊙C上一點,∠BMO=120°,則圓心C的坐標為( )

A. (1,1) B. (1, ![]() ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣![]() ,1)
,1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com