
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點三角形ABC(頂點是網格線的交點)
(1)先將△ABC豎直向上平移5個單位,再水平向右平移4個單位得到△A1B1C1,請畫出△A1B1C1;
(2)將△A1B1C1繞B1點順時針旋轉90°,得△A2B1C2,請畫出△A2B1C2;
(3)求線段B1C1變換到B1C2的過程中掃過區域的面積.

 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:
【題目】向陽中學數學興趣小組對關于x的方程(m+1)![]() +(m﹣2)x﹣1=0提出了下列問題:
+(m﹣2)x﹣1=0提出了下列問題:
(1)是否存在m的值,使方程為一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程為一元一次方程?若存在,求出m的值,并解此方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八(1)班同學為了解2015年某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行如下整理,
月均用水量 | 頻數(戶) | 頻率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
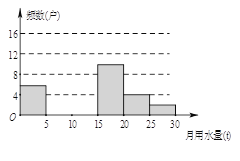
請解答以下問題:
(1)這里采用的調查方式是 (填“普查”或“抽樣調查”),樣本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把頻數分布直方圖補充完整;
,并把頻數分布直方圖補充完整;
(3)若將月均用水量的頻數繪成扇形統計圖,則月均用水量“
(4)若該小區有1000戶家庭,求該小區月均用水量超過10t的家庭大約有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是線段AB上一點,△ACD和△BCE都是等邊三角形,連結AE,BD,設AE交CD于點F.
(1)求證:△ACE≌△DCB;
(2)求證:△ADF∽△BAD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某一工程,在工程招標時,接到甲、乙兩個工程隊的投標書.施工一天,需付甲工程隊工程款1.2萬元,乙工程隊工程款0.5萬元.工程領導小組根據甲、乙兩隊的投標書測算,有如下方案:①甲隊單獨完成這項工程剛好如期完成;②乙隊單獨完成這項工程要比規定日期多用6天;③若甲、乙兩隊合做3天,余下的工程由乙隊單獨做也正好如期完成.試問:
(1)兩隊單獨做各要幾天完成?
(2)在不耽誤工期的前提下,你覺得哪一種施工方案最節省工程款?請說明理.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉村距城市50km,甲騎自行車從鄉村出發進城,出發1小時30分后,乙騎摩托車也從鄉村出發進城,結果比甲先到1小時,已知乙的速度是甲的2.5倍,求甲、乙兩人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】試題分析:設甲的速度是![]() 則乙的速度是
則乙的速度是![]() 甲、乙所用時間分別為:
甲、乙所用時間分別為: ![]() 小時、
小時、![]() 小時;根據題意可得甲比乙多用2.5小時,從而可得關于
小時;根據題意可得甲比乙多用2.5小時,從而可得關于![]() 的方程,解方程即可解答此題;注意,最后要結合題意驗根.
的方程,解方程即可解答此題;注意,最后要結合題意驗根.
試題解析:設甲的速度是![]() 則乙的速度是
則乙的速度是![]() 根據題意列方程,得
根據題意列方程,得
![]() 整理,得
整理,得
![]() ,
,
解得: ![]()
經檢驗, ![]() 是原方程的解.
是原方程的解.
則![]()
答:甲的速度是12km/h,乙的速度是30km/h.
【題型】解答題
【結束】
24
【題目】已知![]() 求
求![]() 的值 。
的值 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】補全下列各題解題過程.
如圖,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度數.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC的頂點坐標為A(﹣2,3)B(﹣3,1)C(﹣1,2),以坐標原點O為旋轉中心,順時針旋轉90°,得到△A′B′C′,點B′、C′分別是點B、C的對應點.
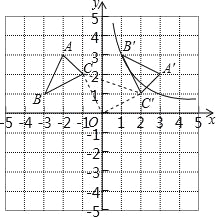
(1)求過點B′的反比例函數解析式;
(2)求線段CC′的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E,F分別是BC,DC上的一個動點,以EF為對稱軸折疊△CEF,使點C的對稱點G落在AD上,若AB=3,BC=5,則CF的取值范圍為 . 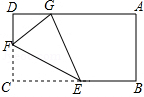
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com